 Sześcian o danej krawędzi a przecięto płaszczyzną przechodzącą przez
trzy jego wierzchołki, a nie zawierają żadnej z krawędzi sześcianu. Znaleźć wysokość
ostrosłupa odciętego tą płaszczyzną od sześcianu.
Sześcian o danej krawędzi a przecięto płaszczyzną przechodzącą przez
trzy jego wierzchołki, a nie zawierają żadnej z krawędzi sześcianu. Znaleźć wysokość
ostrosłupa odciętego tą płaszczyzną od sześcianu.
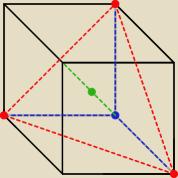 Przekrój − czerwone.
Ostrosłup − czerwone + niebieskie.
Wysokość ostrosłupa − i tu jest problem =D
Ilość ścian ostrosłupa na rysunku − 4
Ilość wysokości ostrosłupa na rysunku = ilość ścian ostrosłupa = 4
Pytanie która wysokość by tu obliczyć =)
Wysokość to odcinek poprowadzony z wierzchołka na na podstawę pod kątem prostym.
Jeżeli za podstawę uznać ścianę należącą do ściany sześcianu ( trójkąt 2 * czerwone +
niebieskie ) to wysokością będzie niebieski odcinek czyli ściana sześcianu. ( trzy takie same
wysokości )
Jeżeli chcemy tą czwartą to będzie to kawałek zielonej kreski − zielona kreska to przekątna
sześcianu = a√3
Przekrój − czerwone.
Ostrosłup − czerwone + niebieskie.
Wysokość ostrosłupa − i tu jest problem =D
Ilość ścian ostrosłupa na rysunku − 4
Ilość wysokości ostrosłupa na rysunku = ilość ścian ostrosłupa = 4
Pytanie która wysokość by tu obliczyć =)
Wysokość to odcinek poprowadzony z wierzchołka na na podstawę pod kątem prostym.
Jeżeli za podstawę uznać ścianę należącą do ściany sześcianu ( trójkąt 2 * czerwone +
niebieskie ) to wysokością będzie niebieski odcinek czyli ściana sześcianu. ( trzy takie same
wysokości )
Jeżeli chcemy tą czwartą to będzie to kawałek zielonej kreski − zielona kreska to przekątna
sześcianu = a√3
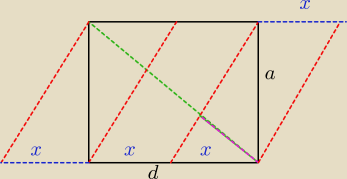 Interesujący nas kawałek to ten różowy − na oko bym rzekł że to 1/3 zielonego ale trzeba to
udowodnić =)
Jak widać na rysunku mamy pewien odcinek ( zielony − D ) sieknięty na trzy kawałki prostymi (
czerwone − h podstawy przekroju ) równoległymi oddalonymi od siebie o x = d/2
Jako że wysokość ostrosłupa zawiera się w zielonym, a podstawa ( patrząc się z tej strony )
jest na tej samej płaszczyźnie co czerwone to zielone jest prostopadłe to czerwonego więc
czerwone będąc odległe od siebie o stałe x siekają zielone na równe części.
Na rysunku widać że części są trzy więc wysokość przekroju:
H= D/3
Powinno być dobrze =)
Interesujący nas kawałek to ten różowy − na oko bym rzekł że to 1/3 zielonego ale trzeba to
udowodnić =)
Jak widać na rysunku mamy pewien odcinek ( zielony − D ) sieknięty na trzy kawałki prostymi (
czerwone − h podstawy przekroju ) równoległymi oddalonymi od siebie o x = d/2
Jako że wysokość ostrosłupa zawiera się w zielonym, a podstawa ( patrząc się z tej strony )
jest na tej samej płaszczyźnie co czerwone to zielone jest prostopadłe to czerwonego więc
czerwone będąc odległe od siebie o stałe x siekają zielone na równe części.
Na rysunku widać że części są trzy więc wysokość przekroju:
H= D/3
Powinno być dobrze =)
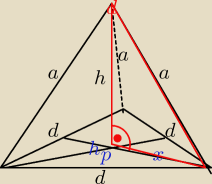 d = a√2, h = ?
d = a√2, h = ?
| 2 | 2 | d√3 | d√3 | a√2*√3 | a√6 | |||||||
x = | hp = | * | = | = | = | |||||||
| 3 | 3 | 2 | 3 | 3 | 3 |
| a√6 | ||
h2 = a2 − ( | )2 | |
| 3 |
| 6a2 | ||
h2 = a2 − | ||
| 9 |
| 9a2−6a2 | ||
h2 = | ||
| 9 |
| a2 | a | a√3 | ||||
h2 = | ⇒ h = | = | ||||
| 3 | √3 | 3 |