Objętość stożka... <prosi>
karolina92:
17 mar 20:55
Jack: co jest dane?
17 mar 20:59
karolina92: już piszę
17 mar 21:00
17 mar 21:02
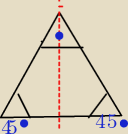
karolina92: Objętość stożka jest równa 125π/3(to jest w ułamku),przekrojem osiowym stożka jest trójkąt
prostokątny. Oblicz promień [podstawy tego stożka.
17 mar 21:02
karolina92: to jest tekst do tego rysunku powyżej. Sorry ale uczę się obsługi
17 mar 21:04
karolina92:
Driver to jest rozwiązanie do tego zadanka

17 mar 21:06
Jack: tylko podstaw

17 mar 21:06
Jack: masz r wyznaczyć, nie V.
17 mar 21:06
driver:
πr3=125π⇒r3=125⇒r=.....
17 mar 21:07
karolina92:
to r=25

17 mar 21:15
karolina92: Dzięki chłopaki posyłam buziaczki

17 mar 21:17
Jack: 
17 mar 21:19
karolina92:
a jak to można rozwiązać?

Suma wysokości walca i promienia jego podstawy jest równa 10cm.
Oblicz jakie największe pole powierzchni bocznej może mieć ten walec.
17 mar 21:47
karolina92:
hejka koledzy jak to zrobić, męczę się nad innymi zadankami , a tego nie ruszę
17 mar 22:04
Jack: r+H=10
Pole boczne to 2πr*H. Zapiszmy r=10−H i podstawmy do wzoru.
P(H)=2π(10−H)*H
Zauważ, że teraz pole P będzie się zmieniało w zależności od H.
Wyobraź sobie że to funkcja że "x" to u nas H. Jak znaleźć rozwiązanie optymalne? Poszukaj
wartości największej dla tej funkcji. Jak się przyjrzysz zobaczysz, że wykresem
P(H)=2π(10−H)*H jest parabola z ramionami opadającymi więc odpowiedź to będzie wierzchołek
paraboli (będzie to najwyższy punkt na paraboli), a dokładnie współrzędna "q" tej paraboli.
17 mar 22:10
karolina92:
chyba tego nie zrobię, mam już mętlik w głowie.
17 mar 22:22
karolina92:

17 mar 22:23
Jack: Zrób coś takiego. Wymnóż te wyrazy.
P(H)=2π(10−H)*H
| | −Δ | |
Potem policz ze wzoru na q= |
| i już będziesz miała.
|
| | 4a | |
Pamiętaj że a to współczynnik to przy H
2, b to współczynnik przy H, c to współczynnik przy
wyrazie wolnym.
17 mar 22:29
karolina92: padam nic na oczy nie widzę nawet proste liczenie sprawia mi już trudność zrobiłam już 45 zadań
i padam.
Pozdrowienia

i lulku.
17 mar 22:51
Jack: jutro ze świeżym umysłem raz, dwa to zrobisz. Pozdrawiam

17 mar 22:53
karolina92: a wyszło mi q=5
17 mar 22:55
Jack: hmm chyba coś z π powinno wyjść... No nic, jutro na to spójrz jeszcze raz

Ale wiesz już jak
robić.
17 mar 22:57
karolina92: nie wiem postaram się a nie daje mi to spokoju, pewno przebudzę się w nocy i będę próbować tak
mam.

17 mar 22:57
Jack: hehe upartaś

Ja kiedyś też tak miałem

17 mar 23:00
karolina92: I nie ruszyłam tego zadania mimo swojego uporu, po prostu nie umiem tego może ktoś mi pomoże
proszę

18 mar 20:49
karolina92:
Proszę o POMOC w tym zadaniu−nic z tego mi nie wychodzi już dwa dni nad nim ślęczę .
Suma wysokości walca i promienia jego podstawy jest równa 10cm. Oblicz jakie największe pole
powierzchni bocznej może mieć ten walec.
18 mar 21:04
Jack: karolina92, wszystko już masz

Spójrz sobie na to równanie
P=2π(10−H)*H
Wyobraź teraz sobie, że pod H podstawiasz różne liczby... mniejsze i większe... Chcesz wstawić
takie H, żeby wynik czyli P było jak największe...
Spróbuj spojrzeć na P=2π(10−H)*H jak na funkcję... Zmienną niech będzie H, a wartością funkcji
P. Czyli niech f(x) to będzie P, a x to będzie H.
f(x)=2π(10−x)*x
Spróbuj to wymnożyć i sobie narysować. Wskaż punkt przyjmujący największą wartość (czyli
największy f(x) ).
18 mar 21:18
karolina92:
18 mar 21:28
karolina92: i obliczam funkcję kwadratową
18 mar 21:29
karolina92: −H2*10H
wynik Δ=10
to
H=5?
18 mar 21:30
karolina92: umarłam

18 mar 21:32
Jack: P(H)=−2π*H
2+20π*H
Δ=(20π)
2
czyli
Punkt q to właśnie wartość tej funkcji, czyli szukane największe pole P.
Coś takiego.
18 mar 21:35
karolina92: czyli zanim zaczęłam kombinować to miałam coś takiego
R=10−x
x*(10−x)=x2*10x
obliczyłam p a nie q i wyszło mi 5 no i rysunek
i P(b)=2πR*x
P(b)= 50π
18 mar 21:44
karolina92:
Jack masz trochę czasu dla mnie jeszcze utknęlam w jednym
18 mar 21:44
karolina92: a za tamto buziaczki

18 mar 21:46
Jack: no fajnie, mi tez tak wyszło

Tylko że jak piszesz już to ostatnie wyrażenie to napisz
P
max=50π
18 mar 21:46
Jack: 
dzięki
18 mar 21:47
karolina92:
18 mar 21:49
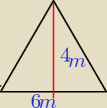
karolina92: Lampa umieszczona na wysokości 4 m nad ziemią oświetla na płaskim terenieobszar 6m.
Oblicz ile metrów wyżej należy zawiesić lampę aby oświetlała obszar 8m.
18 mar 21:51
karolina92: z Talesa mam tak
4m − 6m
xm − 8m
proporcja
x=4}*{86= 5,3
czy teraz mam korzystać z Pitagorasa?
jeżeli tak to nie wychodzi mi to
18 mar 21:55
karolina92: Jack to ja dzięki że mnie nadzorujesz,
18 mar 21:56
Jack:
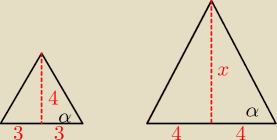
Zauważ, że oba te trójkąty muszą być podobne.
To znaczy, że np. tgα w jednym i drugim Δ musi być taki sam...

18 mar 21:58
Jack: dobrą ułożyłaś proporcję, można też Twoim sposobem.

Zobacz tylko że x to wysokość umieszczenia lampy. Więc musisz policzyć tak naprawdę x−4
("
O ILE wyżej należy zawiesić...")
18 mar 22:00
karolina92: nio o 1,3m ? czyli 5,3?
18 mar 22:12
Jack: Nowa wysokość będzie miała 5,3m ale skoro pytanie dotyczyło tego, o ile należy podnieść
latarkę, to odpowiemy, że o 1,3m
18 mar 22:16
karolina92:
oczywiście

18 mar 22:26
karolina92: Fajowe to forum szkoda, że w ubiegłym roku nie wiedziałam o jego istnieniu

przewalałam kupę zadań z ćwiczeń I i II kl.ale nie musiałam geometrii,więc teraz nadrabiam i
nic zupełnie nie rozumiem. Mam kilkanaście zadań do przerobienia.

Jedne proste i trudniejsze...........,jak dla mnie.
Koniec przerwy zaczynam nowe zadanka.
18 mar 22:33
Jack: Ja też jestem pod wrażeniem ochoty tylu ludzi w niesieniu pomocy innym

18 mar 22:36
karolina92: Szkoda ,że ja się jeszcze nie wykazałam. Myślę, że jak zakończę swój maraton, to będę pomagać.
Lubiłam matmę zawsze, ale i stwarza mi trochę kłopotów.

18 mar 23:04
Jack: może to tyko kwestia czasu

Powodzenia!
18 mar 23:30
karolina92:
Pewno tak

Dziękuję.
Uczysz się? czy jesteś już wyżej?
To nie wścibstwo.....,a może?
pa

18 mar 23:34
Jack: Uczę się na studiach

Nie wścibstwo raczej

18 mar 23:35
karolina92: 
18 mar 23:46
karolina92:
Objętość stożka jest równa 125π3 przekrojem osiowym stożka jest trójkąt prostokątny.
Oblicz promień podstawy tego stożka.
19 mar 19:47
karolina92:
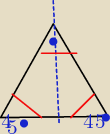
19 mar 19:49
karolina92: to jest rysunek do zadanka.
19 mar 19:50
karolina92: Wiem że go robiliśmy ale powiedziano mi ze mam zle

19 mar 19:51
karolina92: Proszę ETA pomóż

19 mar 20:17
Jack: wiesz co, wczesniej policzylas r3=125 ⇒r=25... Tak się składa, że r=5. NIe przegladałem
wczesniejszych rachunkow ale w tym kroku na pewno mialas blad.
19 mar 21:05
R.W.16l: Poczytałem sobie poczatek i zobaczyłem
r
3=125
r=25
no chyba raczej nie
ps. nie czytałem dalej, więc jeśli jest to już hmm.. "zauważone" to sorry

19 mar 21:17
R.W.16l: no, to było tak ogóolnie potwierdzenie ww wiadomości od
Jack 

19 mar 21:17
Jack: 
to zwieksza prawdopodobienstwo poprawnosci

19 mar 21:18
karolina92: Nio i tak r=5
superrr...,

19 mar 23:04






 Suma wysokości walca i promienia jego podstawy jest równa 10cm.
Oblicz jakie największe pole powierzchni bocznej może mieć ten walec.
Suma wysokości walca i promienia jego podstawy jest równa 10cm.
Oblicz jakie największe pole powierzchni bocznej może mieć ten walec.

 i lulku.
i lulku.

 Ale wiesz już jak
robić.
Ale wiesz już jak
robić.

 Ja kiedyś też tak miałem
Ja kiedyś też tak miałem 

 Spójrz sobie na to równanie P=2π(10−H)*H
Wyobraź teraz sobie, że pod H podstawiasz różne liczby... mniejsze i większe... Chcesz wstawić
takie H, żeby wynik czyli P było jak największe...
Spróbuj spojrzeć na P=2π(10−H)*H jak na funkcję... Zmienną niech będzie H, a wartością funkcji
P. Czyli niech f(x) to będzie P, a x to będzie H.
f(x)=2π(10−x)*x
Spróbuj to wymnożyć i sobie narysować. Wskaż punkt przyjmujący największą wartość (czyli
największy f(x) ).
Spójrz sobie na to równanie P=2π(10−H)*H
Wyobraź teraz sobie, że pod H podstawiasz różne liczby... mniejsze i większe... Chcesz wstawić
takie H, żeby wynik czyli P było jak największe...
Spróbuj spojrzeć na P=2π(10−H)*H jak na funkcję... Zmienną niech będzie H, a wartością funkcji
P. Czyli niech f(x) to będzie P, a x to będzie H.
f(x)=2π(10−x)*x
Spróbuj to wymnożyć i sobie narysować. Wskaż punkt przyjmujący największą wartość (czyli
największy f(x) ).



 Tylko że jak piszesz już to ostatnie wyrażenie to napisz
Pmax=50π
Tylko że jak piszesz już to ostatnie wyrażenie to napisz
Pmax=50π
 dzięki
dzięki

 Zauważ, że oba te trójkąty muszą być podobne.
To znaczy, że np. tgα w jednym i drugim Δ musi być taki sam...
Zauważ, że oba te trójkąty muszą być podobne.
To znaczy, że np. tgα w jednym i drugim Δ musi być taki sam... 
 Zobacz tylko że x to wysokość umieszczenia lampy. Więc musisz policzyć tak naprawdę x−4
("O ILE wyżej należy zawiesić...")
Zobacz tylko że x to wysokość umieszczenia lampy. Więc musisz policzyć tak naprawdę x−4
("O ILE wyżej należy zawiesić...")

 przewalałam kupę zadań z ćwiczeń I i II kl.ale nie musiałam geometrii,więc teraz nadrabiam i
nic zupełnie nie rozumiem. Mam kilkanaście zadań do przerobienia.
przewalałam kupę zadań z ćwiczeń I i II kl.ale nie musiałam geometrii,więc teraz nadrabiam i
nic zupełnie nie rozumiem. Mam kilkanaście zadań do przerobienia. Jedne proste i trudniejsze...........,jak dla mnie.
Koniec przerwy zaczynam nowe zadanka.
Jedne proste i trudniejsze...........,jak dla mnie.
Koniec przerwy zaczynam nowe zadanka.


 Powodzenia!
Powodzenia!
 Dziękuję.
Uczysz się? czy jesteś już wyżej?
To nie wścibstwo.....,a może?
pa
Dziękuję.
Uczysz się? czy jesteś już wyżej?
To nie wścibstwo.....,a może?
pa
 Nie wścibstwo raczej
Nie wścibstwo raczej 







 to zwieksza prawdopodobienstwo poprawnosci
to zwieksza prawdopodobienstwo poprawnosci 
