geometria analityczna Kasia: dany jest punkt A(2,3) i prosta o równaniu x−y−1=0 znajdź wierzchołki B i C równoramiennego trójkąta prostokątnego ABC o przyprostokątnych AB i AC tak aby punkt B należał do prostej i prosa AC była do niej równoległa

Jack: jakieś pomysły masz?

Kasia: dziś na lekcji próbowałam, ale jakoś szybko wróciłam na swoje miejsce, więc nie posiadam pomysłu na to zadanie.:( , a muszę umieć je rozwiązać na następną lekcje

Jack: Zauważ, że skoro przy A ma być kąt prosty, to wskazane będzie poszukac prostej przechodzącej przez ten punkty A, ale równoległej do podanej prostej. Potem znajdź odległość punktu A od prostej (x−y−1=0). Zrób sobie rysunek.

aga: Pomogę Ci Kasiu.

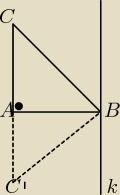
aga: A(2,3), k: x−y−1 = 0 ⇒ y = x − 1 B, C = ?

	1
aAB = −		= −1
	ak

Równanie prostej AB ⊥ k : y − y_A = a_AB(x − x_A) y − 3 = −1*(x − 2) y = −x + 5 Wyznaczamy punkt B z przecięcia się prostych AB i k : (rozwiązujemy układ równań) y = −x + 5 y = x − 1 x−1 = −x+5 2x = 6, x = 3, y = 2, B(3, 2) Wyznaczamy równanie prostej AC II k : a_AC = a_k = 1 y − y_A = a_AC(x − x_A) y − 3 = 1*(x−2) y = x+1 Obliczamy długość boku AB : IABI =√(x_B−x_A)²+(y_B−y_A)² = =√(3−2)²+(2−3)² = √1+1 = √2 C∊ AC , czyli y_C = x_C + 1 IACI = IABI , stąd √(x_C−x_A)² + (Y_C−y_A)² = √2 (x_c − 2)² + (x_C + 1 − 3)² = 2 x_C² − 4x_c +4+x_C² −4x_C +4 −2=0 2x_C² − 8x_C + 6 = 0 /:2 x_C² − 4x_C + 3 = 0 Δ = 16−12=4, √Δ = 2, x_C = 3 lub x_C = 1 y_C=3+1=4 y_C 1+1=2 Czyli C(3,4) lub C'(1,2).