czworotak okrag ewa: POMOCY W czworokącie przekątne są prostopadłe i można w niego wpisać okrąg. Wykaż, że iloczyny długości przeciwległych boków są równe. przynajmniej jakas wskazowke jakby ktos mogl dac.. prosze.. PILNE

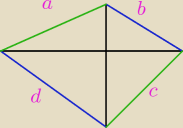
PTwr: Ciocia Wikipedia mówi o okręgu wpisanym w czworokąt "W czworokąt można go wpisać wtedy i tylko wtedy, gdy sumy długości przeciwległych jego boków są równe." Czyli: a+c=b+d A pytanie brzmi czy a*c=b*d czyli czy pola prostokątów zbudowanych z przeciwległych par boków są sobie równe =) To taki początek, zaraz to pomęczę głębiej =)

ewa: bede bardzo dzieczna za to

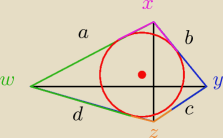
PTwr: Punkty styczności okręgu z bokami czworokąta dzielą każdy bok na dwa fragmenty, fragmenty przy tym samym kącie są sobie równe. ( Dziadek Google mi powiedział =) ) a+c=b+d a*c=b*d a=w+x b=x+y c=y+z d=z+w w+x + y+z = x+y + z+w <−− zgadza się =) (w+x)*(y+z)=(x+y)*(z+w) wy+wz+xy+xz=xz+xw+yz+yw wy i yw się skróci xz i kz też wz+xy=xw+yz −− szaher maher stronami wz−wx=yz−yx −− wspólny czynnik czynnik przed nawias w(z−x)=y(z−x) −− dzielimy przez nawias w≠y I mamy że to jest nieprawda O ile się gdzieś nie ciapłem oczywiście =) Ale w to wątpię bo gdyby takie coś było prawdą to było by we własnościach podane =) Dawno mnie żadne zadanie tak nie zaciekawiło =)

ewa: a skad wiaodmo ze y≠w bo rysunkiem nie koniecznie trezba sie sugerowac.... hm... ?

Wojciech: Też sie nad tym zastanawiałem. Coś nie pasi. DObrze by było PTwr, żebyte przekątne od razu byly dwusiecznymi, wtedy to da się zrobić, hehe.

Wojciech: Może to miał być okrąg opisany na czworokącie? SPrawdź, ewa.

PTwr: hmm, psikus =D Trzeba sprawdzić jeszcze czy y=w Wykorzystać do tego trzeba to że przekątne są sobie prostopadłe Możliwe że przez to wyjdzie że w takim przypadku dwa kolejne boki będą sobie równe ( dwie pary równych boków lub kwadrat/romb =X

ewa: tresc jest dobra

PTwr: W=Y tylko gdy czworokąt jest kwadratem/rombem o ile się nie mylę. Ale okrąg też da się bez problemu wpisać w deltoid, a wtedy W≠Y. Odpowiedź z haczykiem ? hmmm

Wojciech: No to zadanko cukiereczek. Przemyślimy.

PTwr: Gaah! Paintem nie dam rady =X Potrzebuje pejperek zdobyć jakiś =D Zadanko mniam mniam =D Zastanawiam się czy jakoś sinusami i spółą tego nie ugryźć?

ewa: hm.. i doszlicie co to bedzie

Wojciech: mam już rozwiazanie, zaraz podam

PTwr: Ja się wpakowałem w jakiś las używając tych przekątnych =) ciągle liczę =D

PTwr: Zarzuć po czym żeś polazł =>

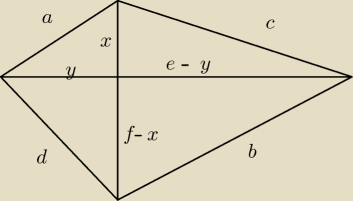
Wojciech: e, f przekątne y² + x² = a² (1) (f − x)² + (e−y)² = b² (2) x² + (e − y)² = c² (3) y² + (f − x)² = d² (4) Dodajemy stronami r−nia (1) z (2) i (3) z (4) y² + x² + f² −2fx + x² + e² −2ey + y² = a² + b² x² + e² −2ey + y² + y² + f² −2fx + x² = c² + d² I odejmujemy stronami, z czego zostaje a² + b² = c² + d² (a + b)² − 2ab = (c + d)² −2cd Okrąg wpisany więc a+b = c+d i zostaje −2ab = −2cd ab = cd c.b.d.u. Zadanko wisienka! Brawo, ewa za nie. Oby więcej takich. Szkoda, że nie ma systemu oceniania zadań.

:o: nie Wojciech brawo za rozwiazanie

ewa: bardzo dziekuje za pomoc

PTwr: Woah =D Więc w połowie skręciłem w labirynt =D Zapisałem to w formie a*b=c*d podstawiając pod a,b,c,d brzydki wzorek z Pitagorasa w stylu √k²+l² i z czterech takich mi horror wyszedł =D

:o: no w matematyce jak sie zle skreci to potrafi czlowieka skrecic

PTwr: Taa =) Mi doszło do tego że przelazłem na figury 3D − cztery graniastosłupy o prostokątach z kawałków przekątnych w podstawach =X Jak do tego doszło to zrezygnowałem z mojej drogi =D