streometria
:o: Kąt rozwarcia stożka ma miarę α. Oblicz miarę łukową kąta środkowego rozwiniętej powierzchni
bocznej tego stożka. Proszę o wytłumaczenie, gdyż nie rozumiem zupełnie tego ? nie wiem czy tu
chodzi o siatkę?
16 mar 18:28
Wojciech:
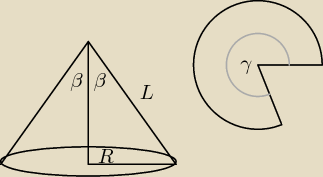
α = 2β
Pytają o kąt γ
Korzystamy z zależności, że:
| πRL | | γ | |
| = |
| chodzi o miarę kąta − 2π lub 360 stopni. |
| πL2 | | 2π | |
16 mar 19:02
:o: nie rozumiem skad sie wziela ta zaleznosc

16 mar 19:05
:o: :((
16 mar 20:48
:o: czy ktos moglby mi wytlumaczyc ?
16 mar 21:04
PTwr: A wyjaśniałem takie coś komuś dzisiaj =) Poszperam w historii =)
16 mar 21:11
:O: bylbym wdzieczny

16 mar 21:17
PTwr: Nie znalazłem =/
l to promień koła z którego wycięto bok
czyli obwód całego koła z którego masz bok to 2πl
obwód podstawy to oczywiście 2πr
po złożeniu widać że obwód wycinka ( czy łuk, nie pamiętam nazwy ) ma taką samą długość jak
obwód podstawy
a więc mamy długość całości i długość kawałka
wiemy że całość ( pełne koło ) to 360 stopni, a w mierze łukowej ( radiany ) 2π ale kąta
kawałka nie znamy
układamy na przykład proporcje
długość kawałka / długość całości = kąt kawałka / kąt całości
2πl / 2πr = x / 2π
l/r = x/2π
x= 2π*l / r
mając kąt rozwarcia wyliczysz r i l z czego wyciągniesz ile tych radianów jest
Jakoś tak
16 mar 21:25
Ramzes: 2π
21 lip 17:01
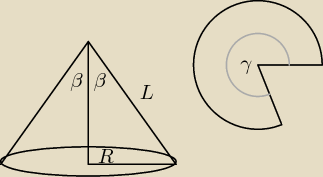 α = 2β
α = 2β

