jeśli na trapezie można opisać okrąg, to jest on równoramienny. aga-baga: Uzasadnij stwierdzenie: jeśli na trapezie można opisać okrąg, to jest on równoramienny.

M:

M:

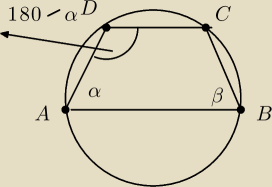
Miś Uszaty: Załózmy że na trapezie ABCD można opisać okrąg Niech ∡| BAD|=α Kat |∡ ABC|=β Z własnosci W dowolnym trapezie suma miar kątów wewnętrzych przy ramieniu jst równa 180^o wynika że |∡ADC| wynosi 180^o−α. Z twierdzenia [Z[Na czworokącie mozna opisac okrąg wtedy i tylko wtedy gdy sumy miar przeciwległych kątów wewnętrznych tego czworokąta sa równe 180^o]] mamy że |∡ABC|+|∡ADC|=β+(180^o−α)=180^o Więc α=β Z własnosci [P[Jeżeli katy przy dowolnej podstawie trapezu maja równe miary to trapez jest równoramienny lub jest porostokątem ]] Trapez ABCD jest trapezem równoramiennym