Wykaż że jeżeli w trapez równoramienny można wpisać okrąg agoo: 12. Wykaż że jeżeli w trapez równoramienny można wpisać okrąg, to wysokość trapezu jest średnią geometryczną długości jego podstaw.

fruu: odswiezam, mam podobne zadanie

Eta:

	a−b
x=
	2

	a+b
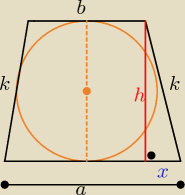
warunek wpisaniaokręgu w trapez: a+b= k+k => k=
	2

z tw. Pitagorasa h²= k² −x² h²= (^a+b₂)² − (^a−b₂)² 4h²= a²+2ab +b² −a²+2ab −b² 4h²= 4ab h²=ab h= √ab c.b.d.o.

fruu: serdecznie dziekuje

Eta:

endrju: no dobrze, ale h=2R, a w trapezie srednia geometryczna podstaw to taki odcinek powiedzmy "y", że a/y = y/b czyli y² = √ab, a jak spróbujemy znaleźć taki odcinek y w tym trapezie to mam wrażenie, że nie będzie on mógł równac się 2R.

arnold: fantastyczne rozwiąznie

kolega arnolda: no rzeczywiście

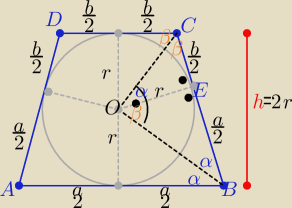
Eta: No to jeszcze inny sposób 2α+2β= 180^o ⇒ α+β= 90^o zatem trójkąt BOC jest prostokątny podobieństwa trójkątów BOE i COE z cechy (kkk)

r		b   2		√ab		√ab
	=		⇒ r2=		⇒ r=		, r>0
a   2		r		4		2

to h=2r= √ab c.n.u

Eta: dla kolegi arnolda

Eta:

	ab
Poprawiam zapis : ⇒ r2=
	4