gh !!!: 406. W kule wpisano dwa stozki o wspolnej podstawie, przy czym jeden z nich ma pole powierzchni bocznej trzy razy wieksze nic drugi. Oblicz stosunek dlugosci wysokosci tych stozkow.

	1
odp:
	9

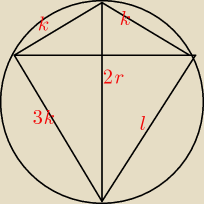
PTwr: Pole powierzchni bocznej stożka to πrl r jest takie same dla obu stożków, nie znamy ich tworzących ( l ) Z oczywistych powodów stożek o większej powierzchni bocznej ma dłuższą tworzącą. l większego zostanie jako l l mniejszego zmutuje w k Jeden ma bok trzy razy obszerniejszy niż drugi więc πrl=3πrk robimy wiadomo co i zostaje l=3k Wysokości obu stożków znajdują się na jednej prostej i razem są równe średnicy kuli ( bo stożki są w nią wpisane i mają tą samą podstawę ) I jak widać na moim paskudnym rysuneczku mamy deltoid, wiemy że jego dłuższa przekątna jest równa sumie wysokości stożków d1=h1+h2 Wiemy że boki deltoidu są w proporcjach 3 do 1 l=3k Masz początek zadania, reszta to pestka =)

!!!: bardzo dziękuję, ale mam problrm nadal, siedzę nad tym od czasu jak odpowiedziałes/aś (czyli już chwilę) i nie wiem nadal co mam z tym dalej zrobić ułożyłam sobie układ z tw. pit: r²+h1²=k² r²+h₂²=9k² −−−−−−−−−−−−−−−−−−−−−− − odjęłam stronami i otrzymałam: h1²−h2²=−9r² ale skąd wziąć jakieś drugie równanie? co dalej?

!!!:

!!!: nie ma co. ja tu pomagam w wolnych chwilach a mi nikt. z resztą widziałam tu już wczoraj podobne stwierdzenie...

!!!: * przepraszam, zwracam honor PTwr i jeszcze raz dziękuję.

!!!: nadal prosze o pomoc

!!!:

Jack: to pionowa oś jest średnicą . może więc k²+(3k)²=(h₁+h₂)² (nie wiem czy już nie zostało to wykorzystane)

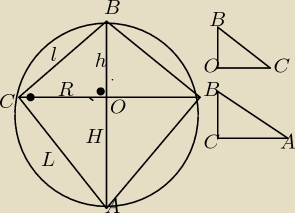
Brochu: D: AB− srednica okręgu czyli |<ACB| = 90^◯ SZ:

h
	=?
H

R: 3πrl=πRL L=3l ΔABC~ΔAOC z cechy KKK (oba są prostokątne i mają wspolny kąt B)

h		l
	=
l		H+h

l² = h(H+h) z tw. pitagorasa w ΔACB: (h+h)² = l²+L² (h+h)² = 10l² podstawiam l² = h(H+h) do drugieog wzoru i mam: (H+h)² = 10h(H+h) / : (h+H) h+H = 10h H=9h Szukany stosunek:

h		h		1
	=		=
H		9h		9