 ?
?  Załóżmy, ze trójkąt ABC jest równoramienny i |AC|=|BC|. Wykaż, że jeśli D∊ AB to suma
odległości punktu D od prostych zawierających boki AC i BC jest równa odległości punktu B od
prostej AC
Załóżmy, ze trójkąt ABC jest równoramienny i |AC|=|BC|. Wykaż, że jeśli D∊ AB to suma
odległości punktu D od prostych zawierających boki AC i BC jest równa odległości punktu B od
prostej AC

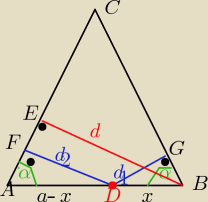 |<A|=|<B|= α ,bo IACI=IBCI IABI=a IADI= a−x IDBI=x
z ΔADF i ΔDGB i ΔABE
|<A|=|<B|= α ,bo IACI=IBCI IABI=a IADI= a−x IDBI=x
z ΔADF i ΔDGB i ΔABE
| d2 | d1 | d | |||
= sinα , | = sinα , | = sinα
| |||
| a−x | x | a |


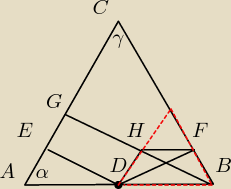 Niech α oznacza kąt BAC, skoro trójkąt jest równoramienny to kąt β oznaczający kąt BAC jest
równy kątowi α.
α=β
Odległość punktu od prostej to odcinek prostopadły do tej prostej.
Na rysunku masz zaznaczone te odległości.
Odcinki ED oraz GB są prostopadłe to odcinka AC gdyż są odległościami punktów od prostej (
zawierającej odcinek AC ) więc ED i GB są sobie równoległe.
Odcinek DH jest prostopadły do odcinka GB ( to jest tu ważne )
Skoro odcinek DH jest prostopadły do GB to jest prostopadły do ED więc jest równoległy do AC
więc prosta w której się zawiera przecina się się z odcinkiem BC pod takim samym kątem pod
jakim odcinek AC styka się z odcinkiem BC, jest to kąt γ.
Z powyższej serii wniosków logicznych wynika że czerwony trójkąt jest równoramienny gdyż dwa
jego boki zawierają się w dwóch odpowiadających bokach trójkąta równoramiennego a trzecia para
boków jest sobie równoległa − więc trójkąty są podobne ( ale to nie jest tu zbyt ważne )
Odcinek HF jest równoległy do DB, więc skoro trójkąt jest równoramienny to wycięliśmy z niego
trapez równoramienny.
Z własności trapezu równoramiennego wynika że jego przekątne są sobie równe, czyli HB = DF.
A skoro DH = EG i z powodu wymienionych wcześniej równoległości i prostopadłości figura GEDH
jest prostokątem to GH = ED.
A skoro GH = ED i HF = DF to ED + DF = GB.
Udowodnione.
Niech α oznacza kąt BAC, skoro trójkąt jest równoramienny to kąt β oznaczający kąt BAC jest
równy kątowi α.
α=β
Odległość punktu od prostej to odcinek prostopadły do tej prostej.
Na rysunku masz zaznaczone te odległości.
Odcinki ED oraz GB są prostopadłe to odcinka AC gdyż są odległościami punktów od prostej (
zawierającej odcinek AC ) więc ED i GB są sobie równoległe.
Odcinek DH jest prostopadły do odcinka GB ( to jest tu ważne )
Skoro odcinek DH jest prostopadły do GB to jest prostopadły do ED więc jest równoległy do AC
więc prosta w której się zawiera przecina się się z odcinkiem BC pod takim samym kątem pod
jakim odcinek AC styka się z odcinkiem BC, jest to kąt γ.
Z powyższej serii wniosków logicznych wynika że czerwony trójkąt jest równoramienny gdyż dwa
jego boki zawierają się w dwóch odpowiadających bokach trójkąta równoramiennego a trzecia para
boków jest sobie równoległa − więc trójkąty są podobne ( ale to nie jest tu zbyt ważne )
Odcinek HF jest równoległy do DB, więc skoro trójkąt jest równoramienny to wycięliśmy z niego
trapez równoramienny.
Z własności trapezu równoramiennego wynika że jego przekątne są sobie równe, czyli HB = DF.
A skoro DH = EG i z powodu wymienionych wcześniej równoległości i prostopadłości figura GEDH
jest prostokątem to GH = ED.
A skoro GH = ED i HF = DF to ED + DF = GB.
Udowodnione.

 i nie pluj
i nie pluj  dziekuje slicznie
dziekuje slicznie

 dziekuje slicznie polapalam sie
dziekuje slicznie polapalam sie jeszcze przeanalizuje i bedzie git dzikeuje za
poswiecony czas
jeszcze przeanalizuje i bedzie git dzikeuje za
poswiecony czas
