matematykaszkolna.pl
pomocy asiek: Oblicz obwód okręgu wpisanego w trójkąt oraz opisanego na trójkącie o bokach długości 2, 3, 4
14 mar 14:05
M:
26 kwi 11:07
M:
17 maj 15:38
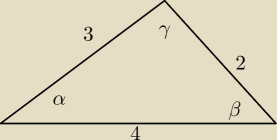
Miś Uszaty: rysunek c2=a2+b2−2a*b*cosγ 16=4+9−2*2*3*cosγ 16=13−12cosγ 12cosγ=−3
 1 
cosγ=−
 4 
 1 
sinγ=√1−
 16 
 √15 
sinγ=
 4 
 1 √15 
PΔ=
*2*3*
=
 2 4 
 3√15 
PΔ=
 4 
 2+3+4 9 
PΔ=r*p p=
=
 2 2 
 PΔ 
r=
 p 
 3√15 2 
r=
*
 4 9 
 √15 
r=
 6 
Obokrwp=2πr
 √15 
Obokrwp=2*π*
 6 
 √15π 
Obokrwp=
 3 
c 
=2R
sinγ 
 4 
4*
=2R
 √15 
16 
=2R
√15 
 16 1 
R=
*
 √15 2 
 8 8√15 
R=
=
 √15 15 
Obokrop=2π*R
 8√15 
Obokrop=2π*
 15 
 16π√15 
Obokrop=
 15 
17 maj 17:09
Mila: Pole Δ:
 9 
p=
− połowa obwodu Δ
 2 
PΔ=√4.5*(4.5−2)*(4.5−3)*(4.5−4)=√135/16
 3√15 
PΔ=
 4 
1) Okrąg wpisany: promień r
3√15 9 
=
*r
4 2 
 √15 
r=
 6 
 π√15 
l=
 3 
2) Okrąg opisany: promień R
3√15 2*3*4 
=
4 4R 
 8 
R=
 √15 
 16π 
L=
 √15 
17 maj 18:26