planimetria maturalna
aga:
Bardzo proszę o pomoc zadaniu, bo już nie mam na nie pomysłu.
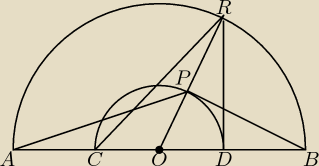
Dane są dwa półokręgi o wspólnym środku O i średnicach odpowiednio AB i CD (punkty A, B, C, D i
O są współliniowe). Punkt P leży na wewnętrznym półokręgu, punkt R leży na zewnętrznym
półokręgu, punkty O, P i R są współliniowe. Udowodnij, że I∡APBI + I∡CRDI = 180
0.
14 mar 00:17
Godzio: to zadanie już było postaram się znaleść
14 mar 00:21
14 mar 00:21
Lachu: OPB = 90 stopni bo jest styczna i tyle

nie mam pomyslu trudne bede myslal dalej
14 mar 00:22
Godzio: widze że mnie ktoś wyprzedził

14 mar 00:25
aga: Dzięki figa, Lachu i Godzio, Ale w moim zadaniu są inne oznaczenia i chodzi
wtedy o inne kąty.
Może ktoś jeszcze wpadnie na pomysł rozwiązania. Bardzo proszę i z góry dziękuję.
14 mar 00:38
aga:
Bogdanie, może pomożesz, bardzo proszę.
14 mar 00:49
aga: 
14 mar 00:58
aga: Błagam.

14 mar 01:57
Bogdan:
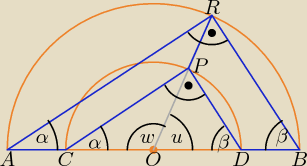
Trójkąty ABR i CDP są podobne.
Podobne są również pary trójkątów: AOR i COP oraz BOR i DOP.
α + β = 90
o
|AO| = |OR| i |CO| = |OP| ⇒ |AC| = |PR|
|BO| = |OR| i |DO| = |OP| ⇒ |DB| = |PR|
Czworokąty: ACPR i BDPR są równoramiennymi trapezami.
Za chwilę ciąg dalszy

14 mar 01:58
Bogdan:
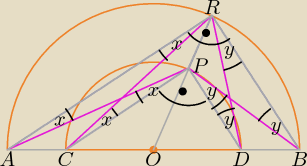
Miarę kąta APB oznaczam a, a = x + 90
o + y,
miarę kąta CRD oznaczam b. x + b + y = 90
o ⇒ b = 90
o − x − y
a + b = x + 90
o + y + 90
o − x − y = 180
o, co należało wykazać.
14 mar 02:11
aga: Dziękuję serdecznie
Bogdanie, że pomimo późnej pory zechciałeś zrobić to zadanie.
Dobranoc, pozdrawiam.

14 mar 02:15
Bogdan:

14 mar 02:22
 Bardzo proszę o pomoc zadaniu, bo już nie mam na nie pomysłu.
Dane są dwa półokręgi o wspólnym środku O i średnicach odpowiednio AB i CD (punkty A, B, C, D i
O są współliniowe). Punkt P leży na wewnętrznym półokręgu, punkt R leży na zewnętrznym
półokręgu, punkty O, P i R są współliniowe. Udowodnij, że I∡APBI + I∡CRDI = 1800.
Bardzo proszę o pomoc zadaniu, bo już nie mam na nie pomysłu.
Dane są dwa półokręgi o wspólnym środku O i średnicach odpowiednio AB i CD (punkty A, B, C, D i
O są współliniowe). Punkt P leży na wewnętrznym półokręgu, punkt R leży na zewnętrznym
półokręgu, punkty O, P i R są współliniowe. Udowodnij, że I∡APBI + I∡CRDI = 1800.
 nie mam pomyslu trudne bede myslal dalej
nie mam pomyslu trudne bede myslal dalej



 Trójkąty ABR i CDP są podobne.
Podobne są również pary trójkątów: AOR i COP oraz BOR i DOP.
α + β = 90o
|AO| = |OR| i |CO| = |OP| ⇒ |AC| = |PR|
|BO| = |OR| i |DO| = |OP| ⇒ |DB| = |PR|
Czworokąty: ACPR i BDPR są równoramiennymi trapezami.
Za chwilę ciąg dalszy
Trójkąty ABR i CDP są podobne.
Podobne są również pary trójkątów: AOR i COP oraz BOR i DOP.
α + β = 90o
|AO| = |OR| i |CO| = |OP| ⇒ |AC| = |PR|
|BO| = |OR| i |DO| = |OP| ⇒ |DB| = |PR|
Czworokąty: ACPR i BDPR są równoramiennymi trapezami.
Za chwilę ciąg dalszy 
 Miarę kąta APB oznaczam a, a = x + 90o + y,
miarę kąta CRD oznaczam b. x + b + y = 90o ⇒ b = 90o − x − y
a + b = x + 90o + y + 90o − x − y = 180o, co należało wykazać.
Miarę kąta APB oznaczam a, a = x + 90o + y,
miarę kąta CRD oznaczam b. x + b + y = 90o ⇒ b = 90o − x − y
a + b = x + 90o + y + 90o − x − y = 180o, co należało wykazać.

