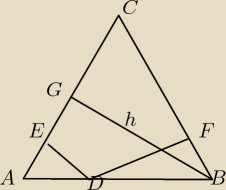
geometria Ewa: Przez dowolny punkt D(różny od wierzchołków należący do podstawy AB trójkąta równoramiennego ABC przeprowadzono proste prostopadłe do ramion, kóre przecinają je w punktach E i F. Wykaż że wysokość poprowadzona na jedno z ramion trójkąta ma długośc równą |DE| + |EF|. zaczęłam to zadanie ale nie wiem czy w dobrym kiedrunku ide z twierdzenia Talesa:

h		DE
	=
AG		AE

DE		DF
	=
AE		FB

z podobieństwa

AG		h
	=
AE		ED

AE		ED
	=
FB		DF

nie wiem co dalej bo porównując to, to nic mi nie wychodzi proszę o pomoc

Lachu: nie masz powiedziane ze h jest rownolegle do DE wiec nie wiem czy dobrze zaczales

Ewa: bo z tego rysunku to nie wynika, ale z punktu D poprowadzono proste prostopadłe do ramion a wyskość tez jest prostopadła do ramienia

Ewa: podpowie ktoś?

Wojciech: fajne zadanko. wydaje się łatwe ale trzeba wpaśc na taki "myk"

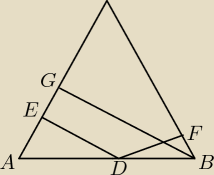Wojciech: Najpierw zauważamy że ∡{ADE} = ∡{BDF} = ∡{ABG} = x

	ED
cosx =
	AD

	DF
cosx =
	DB

	GB
cosx =
	AB

AB = AD + DB

GB		ED		DF
	=		+		// *cosx
cosx		cosx		cosx

GB = h = ED + DF