geometria analityczna Lachu: Obliczyc wspolrzedne pkt P ktory jest rowno odlegly od rzech pkt A=(−1;2) B=(−3;4) C=(5;8)

Lachu: prosze!

bogumill2: moim zdaniem najlepiej wyznaczyc to konstrukcyjnie tzn. nanieś w układzie współrzędnych te trzy punkty następnie połącz je ze sobą tworząc trójkąt. Możesz również narysowac okrąg do którego trzy punkty będą należały .jeśli to zrobisz to zauważysz że prosta BC jest średnicą okregu a jej środek będzie przechodził przez szukany punkt aby go obliczyc skorzystaj ze wzoru s=(x1+x22) (y1+y22)

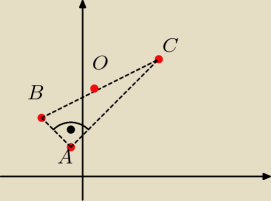
tom: ΔBCA jest prostokątny, więc pkt równoodległy od wierzchołków (czyli środek okręgu opisanego ) leży w połowie przeciwprostokątnej : wektor BC=[8,4] wektorBO=[4,2] stąd O=(1,6)

Lachu: szczerze ja to robilem tak i sprobuje tez Twoja metoda ale zalezaloby mi zeby ktos znalazl mi tutaj blad co robie zle dochodze do tego ze AP=√x2+y2+2x−4y+5 BP=√x2+y2+6x−8y+25 CP=√x2+y2−10x−16y+89 i porownoujac AP=BP wychodzi ze −4x+4y−20=0 i BP=CP to wychodzi 16x+8y−64=0 i nie wychodzi mi z tego ukladu moze mi ktos powiedziec gzie robie bład

Lachu: kurde zebym na takie cos na maturze wpadl dzieki serdeczne .. tom i bogumili2

Bogdan: Punkt P równo odległy od punktów A, B, C jest środkiem okręgu opisanego na trójkącie ABC. Po wstawieniu współrzędnych punktów A, B, C do równania okręgu x² + y² +ax + by + c = 0 otrzymujemy układ równań: a − 2b − c = 5 3a − 4b − c = 25 5a + 8b + c = −89 Jego rozwiązaniem są liczby: a = −2, b = −12, c = 17, stąd mamy ogólne równanie okręgu: x² + y² − 2x − 12y + 17 = 0. Jego środek jest szukanym punktem P. Odp.: P = (1, 6)