planimetria Natalia: Dany jest trójkąt równoramienny ABC o kącie przy wierzchołku C równym 120 stopni. Oblicz pole tego trójkąta, wiedząc, że promień okręgu opisanego na nim jest równy 12. Próbowałam sama coś obliczać i czy to możliwe, by wynik był 452,16?

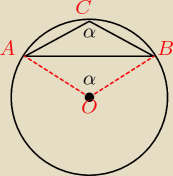
Jack: ΔABC ≈ ΔABO (te same kąty i wspólny odcinek AB) − są przystające. ACBO jest rombem, więc odcinek AB dzieli CO na połowy. Skoro CO jest promieniem, to jego połowa jest wysokością ΔABC. ∡OBC=β jest równy 60^o (z własności rombu). Pole AOBC = a² * sin β Pole trójkąta jest połową pola rombu.

Natalia: Nie wiem ile wynosi a. Z Pitagorasa też mi ewentualnie tylko jakieś √108 wychodzi.

Jack: a to promień R=12.