tom: współrzędne A : y − 2x − 1 =0
−( y − x +3 =0 )
−−−−−−−−−−−−−−−−−−−−−−−−
−x + 2 =0 , x=2 y = 5 A=(2, 5)
prosta k w postaci kierunkowej y=2x+1 prosta m ma postać y=−
12x + b
m po podstawieniu
(4, 1) b
m=3, a równanie m: y=−
12x +3 ' pkt przecięcia z pr. i oblicza sie z ukł. równań
y=−
12x +3 i y − x +3 =0 stąd C=(0, 3)
pole ΔABC najprościej jako połowa modułu wyznacznika pary wektorów BA i BC ( nie wiem jak
narysować strzałkę nad BA I BC

) BA=[−2, 4] BC=[−4, 2]
|−4 2 |
| | 1 | | 1 | |
PΔABC= |
| | | −2 4| | = |
| |−16 + 4| = 6 |
| | 2 | | 2 | |
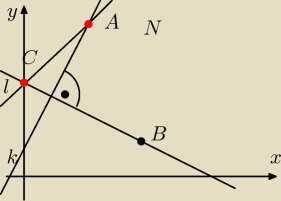 a razie rysunek
a razie rysunek
 ) BA=[−2, 4] BC=[−4, 2]
|−4 2 |
) BA=[−2, 4] BC=[−4, 2]
|−4 2 |
