***GEOMETRIC*** ***GEOMETRIC***: 321 w ostrosłupie prawidłowym czworokątnym wysokość ma długość H, a kąt między ścianami bocznymi ma miarę α. Wyznacz objętość tego ostrosłupa.

	2		α
odp:		H3(tg2		−1)
	3		2

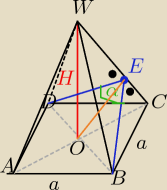
Eta: Pomogę , tak skrótowo (bo strasznie niwygodnie te ułamki pisać , dalej sobie z pewnością poradzisz

	a√2
IOBI = d2=
	2

	IOBI
zΔOBE : tgα2=
	IOEI

	a√2
IOEI=
	2tgα2

z ΔCOE z tw. Pitagorasa : ICEI²= IOCI²−IOEI²

	a2tg2α2− a2
otrzymasz: ICEI2=
	2tg2α2

	a√2*√tg2(α/2)−1
ICEI=
	2tgα2

teraz ΔCOW ~ ΔCOE

	IWOI		IEOI
to:		=
	IAOI		IAEI

podstaw dane otrzymasz: a²= 2H²( tg^2α₂−1) i teraz już tylko do wzoru na V= ........ otrzymasz to co masz w odp Powodzenia

GEOMETRIC: dziękuję bardzo Eto. osobiście dotarłam do momentu, gdzie korzystasz z podobieństwa trójkątów, bo nie umiem udowodnić, że są podobne. Mogłabyś mi wyjaśnić na jakiej podstawie to stwierdzasz (wierzę Ci że tak jest, ale nie daje mi to spokoju )

Eta: Są prostokątne i mają wspólny kąt <OCE

***GEOMETRIC***: 322 Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od jego krawędzi bocznej jest równa d, a krawędź boczna tworzy z płaszczyzną podstawy kąt α. oblicz pole pow. bocznej

	1+2tg2α
odp 2d2		lub dwie alternatywne z sin
	sin2α

zadanie zrobiłam podobnie do powyższego, ale mi nie wyszło. proszę o pomoc

Marcinsztajn: Mogę wiedzieć dlaczego w trójkącie COE zastosowałeś twierdzenie Pitagorasa Przecież to nie jest trójkąt prostokątny...

Dominik: ΔCOE jest prostokatny. |∡CEO| = 90^o

Marcinsztajn: No właśnie że nie jest, na jakiej podstawie tak twierdzisz?