Zadanie z matematyki Kaemo: Proszę o pomoc w rozwiązaniu tego zadania: W równoległoboku o bokach o długości 6 cm i 4 cm oraz kącie ostrym 60^o przeprowadzono dwusieczne kątów. Oblicz obwód czworokąta utworzonego przez punkty przecięcia się wszystkich dwusiecznych.

Eta: Tak mi wyszło z obliczeń Ob= 2(1+√3)

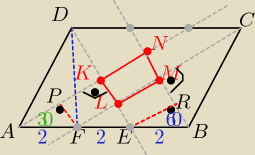
Eta: czworokąt KLMN jest prostokątem! ( tylko krzywo mi się namalował) trójkąt AED jest równoboczny o boku długosci 4 ( stąd wysokość podzieliła boka AB na odcinki 2 i 2,

	IPFI
z trójkącika APF z sin30o=		=> IPFI= IKLI= 1
	2

	IERI
z " " BER z cos 60o=		=> IERI=ILMI= √3
	2

więc prostokat ma wymiary: 1 i √3 to: Ob= 2+2√3= 2(1+√3 cm Sorry , ale wolę liczyć niż rysować ( myślę ,że coś z tego rysunku odczytasz.

Eta: Dodam dla jasności dwusieczne poprowadzone z przeciwległych wierzchołków są równoległe więc odległości między nimi to właśnie długości boków prostokąta KLMN Myślę,że tyle wyjaśnień wystarczy

Eta: Proszę się nie śmiać z mojego "malunku"

Kaemo: dzięki wielkie!

Eta: Kaemo .......Rozumiesz coś z tego?

Maturzysta: Eta mogłabyś spojrzec na moje, bardzo prosze