ss Basia ;): Bardzo prosiłabym o odrobinkę pomocy a dokładniej to o sprawdzenie mojego przykładu Mam za zadanie wyznaczyć PROSTĄ |AB| Punkty: A(−3,−4) B(4,1)

	5		13
i prosta z tych punktów wychodzi mi taka : y=		x−
	7		7

Proszę bardzo o sprawdzenie

Eta: Ok

AS: A gdybyś współrzędne punktów A i B podstawiła do równania sama byś się przekonała czy poprawnie rozwiązałam. Jest poprawnie rozwiazane,ale sprawdz

Basia ;): sprawdziłam tylko mam trochę głupie zadanie i sprawdzam wszystko bo źle mi wynik wychodzi

Basia ;): mam coś takiego xD Może mi trochę pomożecie xD Równoległobok o punktach : A(−3,−4) B(4,1) D(−4,2) oraz C którego nie znam. Więc robię to tak: Wyznaczam sobie prostą AD, następnie prostą równoległą do niej przechodzącą przez punkt B wychodzi mi taka: y=−6x+25 Teraz wyznaczam prostą AB czyli tą tutaj, i równoległą do niej przechodzącą przez punkt D

	5		34
czyli: y=		x+
	7		7

Ostatnim celem jest znalezienie punktu C czyli wyznaczam punkt wspólny przecięcia wyliczonych prostych i wychodzą mi jakieś KOOSMICZNE PUNKTY mógłby mi ktoś jeszcze pomóc z tym ?:(

Basia ;): aaa nie jednak dobrze teraz wyliczyłam x=3 i y=7 wyszło Dzięki za wcześniejszą pomoc

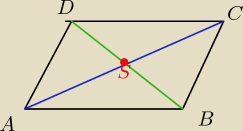
Eta: można prościej: przekątne w równoległoboku dzielą się na połowy,więc S jest środkiem odcinka BD i środkiem odcinka AC

	xB+xD		yB+yD
xS=		... yS=
	2		2

x_S= 0 i y_S= ³₂ teraz x_C= 2x_S − x_A i y_C= 2y_S −y_A x_C= 2*0+ 3= 3 i y_C= 2*³₂+4= 3+4= 7 odp: C( 3,7)

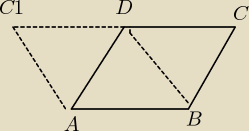
AS: Ale jest jeszcze druga możliwość. Rysunek

Eta: Jest jeszcze taki sposób (najprostszy ze wszystkich ) → → wektory AB = DC to → → AB=[7,5] i DC = [x_C+4, y_C−2] zatem: x_C+4=7 i y_C−2=5 x_C= 3 i y_C= 5 C( 3,5) Pozdrawiam AS