kwadratówka parametr
Malaa: zbadaj liczbę rozwiązań równania ze względu na wartość parametru m (m eR). napisz wzór i
narysuj wykres funkcji y=g(m), która każdej wartości parametru m przyporządkowuje liczbę
rozwiązań równania:
(m−3)x
2 + (m−2)x+1 = 0
Δ= m
2 − 8m + 16
Δm= 0
i teraz obliczam x0

gubię się cały czas.......
11 mar 01:29
Godzio: ty nie masz obliczać x tylko parametr m dla którego istnieje rozwiązanie
11 mar 01:31
Eta:
Δ= m2−8m+16= (m−4)2
dla m€R\{4} są dwa rózne rozwiązania
dla m= 4 −− jedno rozwiązanie
11 mar 01:33
Godzio:
Jeśli funkcja kwadratowa:
m≠3
Δ = m2 − 4m + 4 − 4(m−3) = m2 − 4m + 4 − 4m + 12 = m2 − 8m + 16 = (m−4)2
1o Jeśli Δ > 0 to funkcja f(x) ma 2 rozwiązania
(m−4)2 > 0
m∊R − {3,4}
2o Jeśli Δ = 0 to funkcja f(x) ma 1 rozwiązanie
(m−4)2 = 0
m = 4
3o Jeśli Δ < 0 to funkcja f(x) ma 0 rozwiązań
m∊∅
Jeśli funkcja liniowa to funkcja f(x) ma 1 rozwiązanie
m = 3
11 mar 01:34
Malaa: czyli m
o =8/2 = 4
czyli dla
2 rozwiązań m e R −{3,4}

?
11 mar 01:34
Malaa: ok.. teraz dopiero przeczytałam to co napisałeś..
11 mar 01:35
Eta:
O, tak
Godzio
nie popatrzyłam na wspłczynnik "a"
11 mar 01:36
Godzio:
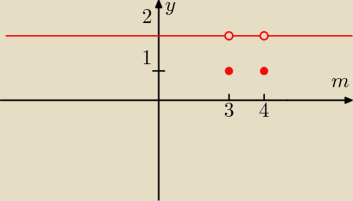
11 mar 01:38
Godzio: 
11 mar 01:38
Godzio: mam nadzieje że pomogłem

a teraz już idę wypocząc
Dobranoc

11 mar 01:41
Malaa: (m−4)2 > 0
a mógłbyś mi to jeszcze rozpisać ? żebym nie miała już żadnych wątpliwości.. to chyba nie jest
już dobra godzina na myślenie.
11 mar 01:42
Malaa: hehehe

ok, dobranoc

11 mar 01:43
Malaa: i dzięęęki : ) !
11 mar 01:43
 gubię się cały czas.......
gubię się cały czas.......
 ?
?
 nie popatrzyłam na wspłczynnik "a"
nie popatrzyłam na wspłczynnik "a"


 a teraz już idę wypocząc
Dobranoc
a teraz już idę wypocząc
Dobranoc 
 ok, dobranoc
ok, dobranoc 