m
:(: 1) Krawędź podstawy w ostrosłupie prawidłowym czworokątnym ,a długość 8 cm a kąt między
płaszczyznami, w których zawierają się przeciwległe ściany boczne, ma miarę 700. Oblicz: a)
pole powierzchni całkowitej ostrosłupa b) objętość ostrosłupa Wyniki zaokrąglij do dwóch
miejsc po przecinku
2) Podstawą ostrosłupa czworokątnego jest kwadrat o boku a. Jedna z krawędzi bocznych jest
prostopadła do podstawy ostrosłupa, a dwie są nachylone do płaszczyzny podstawy pod kątem
450. Oblicz cosinus kąta α nachylenia najdłuższej krawędzi bocznej do płaszczyzny podstawy
10 mar 23:43
:(: Help me please

!
10 mar 23:56
Basia: rysuję i pomagam
10 mar 23:58
Basia:
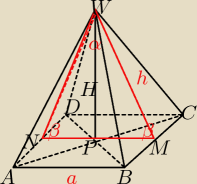
a=8
α=70
tr.NWM jest równoramienny
2β=180−α=110
β=55
tr.MPW jest prostokatny
H
2+(a/2)
2=h
2
znajdź te sinusy w tablicach i wykonaj obliczenia
11 mar 00:08
Basia:
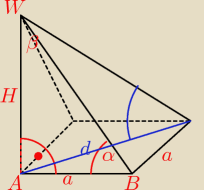
α=45 ⇒ tr.BAW jest prostokątny równoramienny, bo β=90−α=45 ⇒
H=a
d jest przekątną kwadratu o boku a
d=a
√2
tr.CAW jest prostokątny
| | AW | | H | | a | | 1 | |
tgγ= |
| = |
| = |
| = |
| |
| | AC | | d | | a√2 | | √2 | |
√2*sinγ=cosγ
sin
2γ+cos
2γ=1
sin
2γ+2sin
2γ=1
3sin
2γ=1
11 mar 00:17
:(: | | √6 | |
w odpowiedziach pisze ze cos α= |
| |
| | 3 | |
11 mar 00:21
Basia: i dobrze jest, bo na końcu się pomyliłam, zamiast
√2 napisałam 2;
ma być:
| | √2*√3 | |
cosγ=√2*sinγ= |
| =√6{3} |
| | 3 | |
11 mar 00:29
Bogdan:
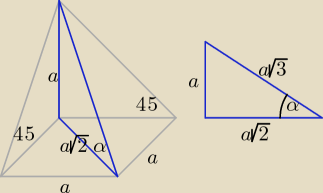
11 mar 00:29
:(: dziekuje

za pomoc
11 mar 01:12
 !
!
 a=8
α=70
tr.NWM jest równoramienny
2β=180−α=110
β=55
a=8
α=70
tr.NWM jest równoramienny
2β=180−α=110
β=55
 α=45 ⇒ tr.BAW jest prostokątny równoramienny, bo β=90−α=45 ⇒
H=a
d jest przekątną kwadratu o boku a
d=a√2
tr.CAW jest prostokątny
α=45 ⇒ tr.BAW jest prostokątny równoramienny, bo β=90−α=45 ⇒
H=a
d jest przekątną kwadratu o boku a
d=a√2
tr.CAW jest prostokątny

 za pomoc
za pomoc