Oblicz długość przekątnych rąbu o kącie ostrym 60* i polu równym ABCD: Oblicz długość przekątnych rąbu o kącie ostrym 60* i polu równym 32√2 cm²

Tomek.Noah: dluzsza ma 8√6 druga 8√2

ABCD: A jak do tego doszłeś?

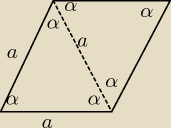
Tomek.Noah: α=60^o jak widac mamy 2 trojkaty rownoboczne P=32√2 P=2*P_Δ (troj.)

	a2√3		a2√3
P=		*2=
	4		2

a2√3
	=32√2
2

a²√3=64√2

	64√6
a2=
	3

	64√6
a=pierwiastek a pod nim		=8*614*312*3−13=8√2
	3

zatem jedna przekatna ma dl 8√2 a dluzsza ma: skoro jest romb podzielony na 2 trj rownoboczne to jego przekatna jest pdwojona wysokoscia troj rownobocznego

	a√3
2*		=a√3=8√6
	2