Problem Alv: Wyznacz zbiór wartości funkcji: f(x)=|x − 1| + |x + 4| Mam z tym problem, wydaje mi się że powinienem rozpatrzyć 4 przypadki zrobić wykres i odczytać zbiór wartości, ale nie wychodzi tak jak powinno. Mógłby ktoś pomóc? Zrobiłem tyle: I x−1≥0 x+4≥0 z tego x ∊ <1, ∞) II x−1≥0 x+4<0 x ∊ (−∞, −4) ∪<1, ∞) III x−1<0 x+4≥0 x ∊ <−4, 1) IV x−1<0 x+4<0 x ∊ (−∞, −4) Widzę, że przedział x ∊ (−∞, −4) ∪ <1, ∞) pokrywa się z dwoma innymi, ale powstaje w tym przypadku zupełnie inny wzór funkcji, więc wnioskuję że zapomniałem czegoś uwzględnić? Dowiedziałem się że powinny być tylko 3 przedziały: 1. x ∊ (−∞, −4) 2. x ∊ <−4, 1> 3. x ∊ (1, +∞) Ale czemu nie 4?

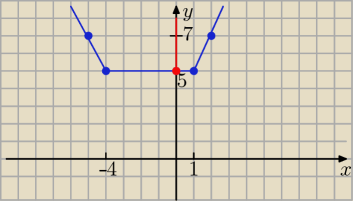
Eta: miejsca zerowe pod modułami x−1=0 => x =1 i x +4=0 => x = −4 rozpatrujesz trzy przedziały I II III −−−−−−−−−(−4)−−−−−−−−−−−−−−−(1)−−−−−−− 1/ x€( −∞, −4) 2/ x€ <−4,1) 3/ x€ <1,∞) 1) dla x€( −∞, −4) f(x) = −x+1−x−4= −2x −3 2) dla x€<−4,1) f(x)= −x +1 +x +4 = 5 3) dla x€<1,∞) f(x) = x−1 +x+4= 2x +3 { −2x−3 dla x €(−∞, −4) f(x)= { 5 dla x€<−4,1) { 2x +3 dla x€<1,∞) ZW= <5,∞)