MM
M: Zad. 1 Wysokość ostrosłupa prawidłowego czworokątnego ma długość 8 cm. Krawędź boczna jest
nachylona do płaszczyzny podstawy pod kątem 450. Oblicz: a) objętość ostrosłupa b) pole
powierzchni bocznej ostrosłupa
Zad 2. Ściana boczna w ostrosłupie czworokątnym prawidłowym tworzy z płaszczyzną podstawy kąt o
mierze 500. Wysokość jego ściany bocznej ma długość 10 cm. Oblicz pole powierzchni bocznej
ostrosłupa.
Zad 3 W ostrosłupie prawidłowym czworokątnym przeciwległe krawędzie boczne o długościach 2√2 są
do siebie prostopadłe. Oblicz objętość tego ostrosłupa.
Zad 4 Krawędź podstawy w ostrosłupie prawidłowym czworokątnym ,a długość 8 cm a kąt między
płaszczyznami, w których zawierają się przeciwległe ściany boczne, ma miarę 700. Oblicz: a)
pole powierzchni całkowitej ostrosłupa b) objętość ostrosłupa Wyniki zaokrąglij do dwóch
miejsc po przecinku
Zad. 5 Oblicz rzeczywistą powierzchnię piramidy w kształci ostrosłupa prawidłowego
czworokątnego o wysokości 120m, wiedząc że na planie w skali 1:5000 krawędź jej podstawy ma
długość 64 mm. O ile procent powierzchnia boczna piramidy jest większa od powierzchni jej
podstawy?
Zad. 6 Podstawą ostrosłupa czworokątnego jest kwadrat o boku a. Jedna z krawędzi bocznych jest
prostopadła do podstawy ostrosłupa, a dwie są nachylone do płaszczyzny podstawy pod kątem 450.
Oblicz cosinus kąta α nachylenia najdłuższej krawędzi bocznej do płaszczyzny podstawy.
Zad. 7 W sześcianie o krawędzi długości a połączono wszystkie wierzchołki dolnej podstawy z
jednym z wierzchołków podstawy górnej. Sporządź odpowiedni rysunek i oblicz pole powierzchni
całkowitej otrzymanego w ten sposób ostrosłupa. Z ilu takich ostrosłupów można złożyć
sześcian?
10 mar 18:32
Szymon :
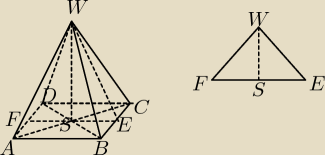
WS=8
∡ FEW=EFW = 45
o
∡FWE=90
o
SE=8
z tw pitagorasa:
WS
2+SE
2=WE
2 ⇒
√64+64=WE ⇒ WE=
√128=8
√2
FE=2*SE=16
FE=AB=BC
| | 1 | | 1 | | 2048 | |
V= |
| AB2*WS ⇒ V= |
| 162*8 ⇒ V= |
| |
| | 3 | | 3 | | 3 | |
P
pc−pole pow całkowitej
P
b−pole boczne
P
s−poleś ściany bocznej
P
p−pole podstawy
P
pc=P
p+P
b
P
p=AB
2=256
P
b=4*P
s
| | 1 | | 1 | |
Ps= |
| *BC*WE ⇒ |
| *16*8√2=64√2 |
| | 2 | | 2 | |
P
p=4*64
√2=256
√2
P
c=256+256
√2=256(1+
√2)
10 mar 18:55
Szymon : jaa to jest źle źle przeczytałem zadanie wybacz już poprawiam
10 mar 18:57
Szymon :
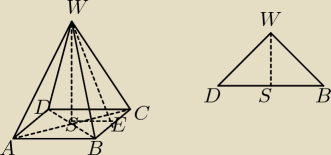
zad 1
kąt DBW=BDW= 40
o
analogicznie jak wyżej:
WS=8
SB=8
DB=16=AB
√2
WB
2=SB
2+WS
2
WB=8
√2
AB=8
√2
P
p−pole podstawy=AB
2 ⇒ P
p=128
WE
2=SE
2+WS
2 ⇒ WE=
√96=4
√6
| | 1 | | 1 | |
Ps= |
| *BC*WE ⇒ Ps= |
| * 8√2*4√6=4√12 |
| | 2 | | 2 | |
P
b=16
√12=32
√3
powinno być ok
10 mar 19:14
 WS=8
∡ FEW=EFW = 45o
∡FWE=90o
SE=8
z tw pitagorasa:
WS2+SE2=WE2 ⇒ √64+64=WE ⇒ WE=√128=8√2
FE=2*SE=16
FE=AB=BC
WS=8
∡ FEW=EFW = 45o
∡FWE=90o
SE=8
z tw pitagorasa:
WS2+SE2=WE2 ⇒ √64+64=WE ⇒ WE=√128=8√2
FE=2*SE=16
FE=AB=BC
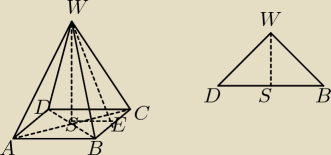 zad 1
kąt DBW=BDW= 40o
analogicznie jak wyżej:
WS=8
SB=8
DB=16=AB√2
WB2=SB2+WS2
WB=8√2
AB=8√2
Pp−pole podstawy=AB2 ⇒ Pp=128
zad 1
kąt DBW=BDW= 40o
analogicznie jak wyżej:
WS=8
SB=8
DB=16=AB√2
WB2=SB2+WS2
WB=8√2
AB=8√2
Pp−pole podstawy=AB2 ⇒ Pp=128