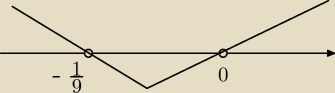
nierówności gimigis: mam takie głupie zadania: 1. 9^x + 3^x−2 > 0 i zastosowałam tu ''t'' i wyszło mi t = 0 oraz t = −1/9 chciałam zaznaczyć na osi i wyszło mi coś takiego jak wyżej... i dalej mnie już zablokowało, bo o ile się nie mylę to powinno być,że t ∊ (−∞,0)U(1/9,∞)

	7		1
2. 2x −		−		< 0
	4		4x

Sabin: Jeśli podstawiłaś za t = 3^x, to pamiętaj, że t > 0, więc nie możesz mieć w rozwiązaniu t mniejszych od zera.

gimigis: to jak to zadanie powinno wyglądać

Sabin: t = 3^x Po pierwsze, jesli juz to jakos tak. Po drugie, z tego odpowiedz to t ∊ (−∞, −¹₉) ∪ (0, +∞) Uwzgledniajac to, ze t > 0 masz: t ∊ (0, +∞) Czyli 3^x ∊ (0, +∞) 3^x > 0, a to zachodzi dla każdego rzeczywistego x, czyli odpowiedź x ∊ R.

gimigis: faktycznie pomyliłam ten wykres

gimigis: a tego z tym − 1/9 nie biorę pod uwagę

Jack: 1. funkcja wykładnicza jest zawsze większa od 0 wiec jak sumujesz dwie takie funkcje to zawsze masz wynik większy od zera. Stąd x ∊ R. 2. podstaw za t=2^x , t≥0.

Sabin: Nie bierzesz, bo t = 3^x i jako funkcja wykładnicza t NIE MOŻE BYĆ UJEMNE, zgodnie z tym, co napisał Jack.

gimigis: chciałam wiedzieć jedną rzecz, jak zapisałam sobie to 3^x ∊ (0,∞) to jak zapisać i wyliczyć dla (−∞,−1/9)

gimigis: oki,rozumiem

gimigis: ale powiedzcie mi czy w ogóle dobrze to wyliczyłam,bo może inaczej powinno wyjść

Jack: Wykres jest niepotrzebny na dobrą sprawę Wystarczy skorzystać z własności funkcji wykładniczej (jest ZAWSZE, tzn dla każdego x, większa od 0).

gimigis: a możesz mi tylko powiedzieć czy w tym drugim czasem nie wyjdzie Δ

Jack: Podstawienie t=2^x, t≥0.

	7		1
t−		−		<0 \* t2
	4		t2

	7
t3−		t2−1<0
	4

No i trzeba znaleźć jakieś rozwiązanie Jednak nie z Delty, bo nie mamy wyrażenie kwadratowego...

gimigis: nio właśnie...nie wiedziałam czy pomnożyć przez samo t czy t²

gimigis: kurcze nie wiem...próbowałam wyciągnąć przed nawias,ale to chyba jakieś głupoty wyjdą...

	1
t2(t − 7/4 −		)
	t2

gimigis: chyba już wiem

Jack:

gimigis: chociaż nie myślałam,że wyciągnę przed nawias samo t i w nawiasie wyjdzie mi delta,ale nie wiem,proszę poradź

Jack: hm... masz odpowiedź do tego? Jesli jest fikuśna, to możliwe ze trzeba skorzystać z http://pl.wikipedia.org/wiki/Równanie_sześcienne#Wszystkie_rozwi.C4.85zania:_wzory_Cardano

gimigis: jesteś

gimigis: konkretnie zadanie brzmi: wyznacz największą liczbę całkowitą spełniająca nierówność i w odp. jest 0

gimigis: wiesz co to co mi podałeś to pierwszy raz na oczy widzę i nie moge tego zastosować,może jest jakiś inny sposób...

Jack: To polecenie zmienia postać rzeczy... Skoro największą, to zauważ, że im większy x, tym

	1
wyrażenie większe... Im mniejszy x, to wyrażenie też rośnie bo		.
	4x

Czyli funkcja rośnie. Ja bym to zrobił podstawiając liczby zaczynając od czegos w okolicach zera, żeby pozbyć się elegancko funkcji wykładniczych... Zauważysz (wpadniesz na pomysł), że x=1 jest rozwiązaniem

	1
tego równainia, czyli 2x−U[7}{4}−		dla x=1 się zeruje. Stąd, skoro była to funkcja
	4x

rosnaca, to największą liczbą całkowitą spełniającą nierówność jest x=0 (tzn liczba troszkę mniejsza od 1, ale najbliżej 1 po lewej stronie jest 0).

Jack:

	1
poprawka.... Im mniejszy x, to wyrażenie MALEJE (STOI "−" przed		) Poza tym ok.
	4x

Eta,Godzio może wy poradzicie: na lekcji było podobne zadanie,wyliczyliśmy x i na końcu wyznaczyliśmy ta największą liczbę,ja zwyczajnie chce wyliczyć ten głupi x

Sabin: ech... t³ −⁷₄t² − 1 < 0 /*4 4t³ − 7t² − 4 < 0 zapisuję −7t² jako −8t² + t² 4t³ − 8t² + t² − 4 < 0 4t²(t − 2) + (t − 2)(t + 2) < 0 (t − 2)(4t² + t + 2) < 0 z drugiego nawiasu Δ = 1 − 4*4*2 < 0, czyli 4t² + t + 2 jest zawsze dodatnie. (t − 2)(4t² + t + 2) < 0 /: 4t² + t + 2 t − 2 < 0 t < 2 2^x < 2 x < 1 Największą liczbą całkowitą mniejszą od 1 jest 0. Stąd x = 0.

Jack:

Eta,Godzio może wy poradzicie: dzięki wielkie Sabin Tobie Jack też

Eta,Godzio może wy poradzicie: ale wiesz co tej delty nie czaje

Jack: tzn?

Sabin: Tak czekałem na to pytanie... Δ wyszła ujemna, co znaczy że wykres paraboli 4t² + t + 2 leży w całości NAD osią t (osią "iksów"). A to znaczy, że 4t² + t + 2 jest ZAWSZE wartością dodatnią, niezależnie jakie t tam wstawisz. Skoro tak, to możesz przez to podzielić, bo to jest tak samo, jakbyś dzieliła przez jakąkolwiek liczbę dodatnią, np. 5 albo 12938761.

Eta,Godzio może wy poradzicie: nio wychodzi √Δ = √31

Eta,Godzio może wy poradzicie: nio ujemna

Sabin: Δ = −31, więc żadnego √Δ mieć nie będziesz

Eta,Godzio może wy poradzicie: nie krzycz zapomniałam że to będzie − 31 a nie 31

Eta,Godzio może wy poradzicie: zadam jeszcze jedno pytanie,może głupie,ale ważne nie da się tego inaczej zrobić na lekcji to jakoś inaczej wygląda

Eta,Godzio może wy poradzicie: zostawię tak jak jest,bo rozumiem to,ale myślę,że można to jeszcze jakoś inaczej zrobić dzięki za pomoc