 szukany punkt C( x,y)
IBCI= 4√3 IABI= 4
ze wzoru cosinusów
ICBI2= IABI2+ IACI2 −2IABI*IACI*cosα
48= 16+IACI2 −2*4*IACI*cos120o , cos120o= −cos60o= −u{1}{2]
IACI2+4IACI−32=0 Δ= 144 √Δ= 12
IACI= 4
więc trójkąt ABC jest równoramienny IACI= IABI=4
to:
IACI2 = x2+y2= 16
i
IBCI2 = x2+(y−4)2= (4√3)2 = 48
x2+ y2−8y+16= 48
16 − 8y+16= 48 => −8y= 16 => y= −2
to x2+(−2)2= 16 => x2= 12 => x = −2√3 v x= 2√3
to są dwa takie punkty spełniające warunki zadania :
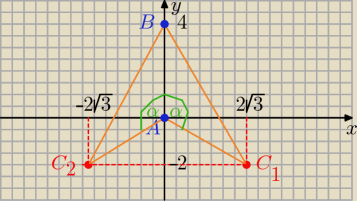
C1( −2√3,−2) i C2( 2√3, −2)
szukany punkt C( x,y)
IBCI= 4√3 IABI= 4
ze wzoru cosinusów
ICBI2= IABI2+ IACI2 −2IABI*IACI*cosα
48= 16+IACI2 −2*4*IACI*cos120o , cos120o= −cos60o= −u{1}{2]
IACI2+4IACI−32=0 Δ= 144 √Δ= 12
IACI= 4
więc trójkąt ABC jest równoramienny IACI= IABI=4
to:
IACI2 = x2+y2= 16
i
IBCI2 = x2+(y−4)2= (4√3)2 = 48
x2+ y2−8y+16= 48
16 − 8y+16= 48 => −8y= 16 => y= −2
to x2+(−2)2= 16 => x2= 12 => x = −2√3 v x= 2√3
to są dwa takie punkty spełniające warunki zadania :
C1( −2√3,−2) i C2( 2√3, −2)