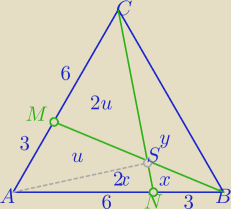
Oblicz pole trójkąta równobocznego NBS. GTomo: Dany jest trójkąt równoboczny ABC o boku długości 9. Wybrano punkty M i N, należące odpowiednio do boku AC oraz AB, w taki sposób, że ∣AM∣=∣NB∣=3. Odcinki MB oraz NC przecięły się w punkcie S. Oblicz pole trójkąta NBS.

Mila: 1) ΔNBS nie jest trójkątem równobocznym. 2) Jeden ze sposobów: P_ΔABC=P

	1
3x+u=		P /*(−3)
	3

	2
2x+3u=		P
	3

============ −9x−3u=−P

	2
2x+3u=		P
	3

	1
−7x=−		P
	3

	1
x=		P
	21

	1		92√3
[NBS]=		*		=..
	21		4

.: odrobinę szybciej będzie zauważyć (porównujemy pola 2*P_ABM = P_BMC):

	1
2*(x+2x+u) = 2*		P = 2u + y −−−−> 6x = y
	3

natomiast z P_BNC:

	1		1		1
x+y =		P −−−> 7x =		P −−−> x =		P
	3		3		21

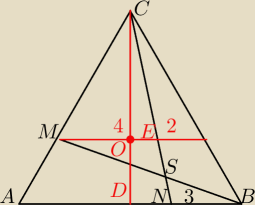an: można tak △MES podobny do △NSB w skali 3/4

	1		3√3
OD=		CD =
	3		2

wysokość △NSB

	3		9√3
h=		OD=
	7		14

	3		9√3		27√3
P=				=
	2		14		28