proszę o rozwiązanie anna: w trójkącie ABC poprowadzono dwusieczne kąta BAC która przecina bok BC w punkcie D W trójkąty ABD i ACD wpisano okręgi, które są styczne z odcinkiem AD w punktach odpowiednio M i N oblicz długość odcinka MN wiedząc że I AB I = 9 I BC I = 5 I AC I = 6

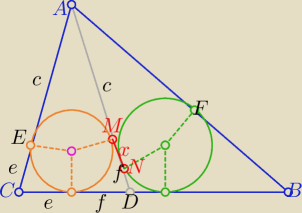
Eta: Z tw. o dwusiecznej:

	AC		CD
		=		|CD|=y
	AB		DB

	6		|y
		=		⇒y=2=|CD| to |DB|=3
	9		5−y

|AD| =d−−− dł dwusiecznej ( z tw. Stewarta) d²= |AC|*|AB|− |CD|*|DB| d²= 6*9−2*3 d= 4√3 |MN|= |AN|−|AM| Z tw. o odcinkach stycznych:

	obwód ACD
|AN|=		−|CD|
	2

	6+4√3+2
AN=		−2 = ... = 2+2√3
	2

analogicznie:

	ObwódDAB
|AM|=		−|DB|
	2

	9+4√3+3
|AM|=		−3
	2

|AM|=3+2√3 to |MN|= 1 =======

Eta: Poprawiam zapisy:

	obwódACD
|AM|=		−|CD|
	2

	obwód DAB
i |AN|=		−|DB|
	2