podpowiedz ~~paw: Dany jest ostrosłup trójkątny ABCS, w którym krawędzie BS i CS mają długość 5, a każda z pozostałych krawędzi tego ostrosłupa ma długość 8. Prosze o podpowiedz, jak będzie wygladac wysokośc w tym ostrosłupie krawedz AS? W podstawie bedzie równoboczny trojkąt 8x8x8 tak?

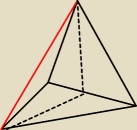
menda: AS masz na czerwono, jest długości 8. Ściana BCS jest prostopadła do podstawy, czyli między przerywanymi liniami jest ∡90. W podstawie jest trójkąt równoboczny o krawędzi 8.

.: Menda −−− Bzdura ... to nie tak wyglądać będzie ten ostrosłup! Absolutnie nie będzie tam kąta prostego

~~paw: Ktoś coś wie?

~~paw: njie trzeba juz wiem

~~kat: menda zrobiła ok

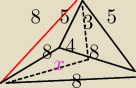
~~beb: menda jest żle choć ta wysokośc tak wyglada ale gdy wyliczam wychodzi bzdura bo hs²+4²=5² hs=3 i potem hpodstwy=4√3 i powinno z pitagorasa zadzialac ze 3²+(4√3²=8² co jest głupotap

~~beb: czyli jak to bedzie?

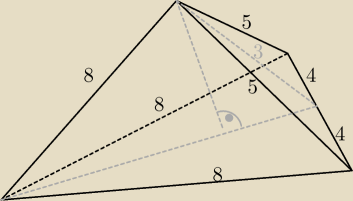
.: Tak będzie wyglądał.

.: I mamy układ równań: (4√2 − x)² + H² = 8² x² + H² = 3² (4√2 − x)² − x² = 8² − 3² 32 − 64 + 9 = −2x a więc ostrosłup ten jeszcze będzie inaczej wyglądać ... bo będzie to tak:

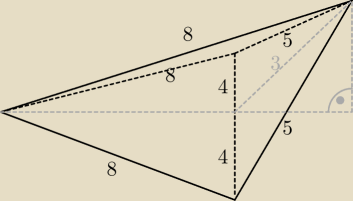
.: i mamy poprawny układ równań: (x+4√2)² + H² = 8² x² + H² = 3² co daje nam: 32 + 8√2x = 8² − 3² 8√2x = 23

	23√2
x =
	16

.: kurdę ... błąd znowu ... nie 4√2 tylko 4√3 powinno być ... więc: 8√3x = 64 − 9 − 48 8√3x = 5

	5√3
x =
	24

~~beb: eh, może ktoś jakoś lepiej to wyjasni

maks: https://www.youtube.com/watch?v=vQ3efHPEFV0 wszystko pieknie wytlumaczone