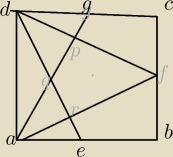
kwadrat geometria ~~ooolii: z matury próbnej nie mam pojecia od czego zaczac zrbilem podział obszaru szukanego na dwa trojkaty, Punkty E, F, G są odpowiednio środkami boków AB, BC oraz CD kwadratu ABCD. Odcinki AG i DF przecinają się w punkcie P, odcinki AG i DE przecinają się w punkcie Q, a odcinki AF i DE przecinają się w punkcie R

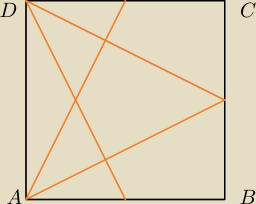.: No dobrze ... ale jaka jest treść zadania? Co należy zrobić w tym zadaniu

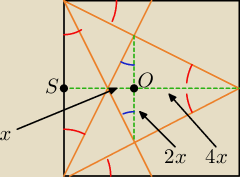.: jeżeli masz policzyć jaką część pola kwadratu ABCD stanowi pole trójkąta PQR to: 1. dorysujmy jeszcze zielone równoległe do boków kwadratu i wprowadźmy dwa nowe punkty (S i O)

	1
2. zauważmy, że czerwone kąty są sobie równe, ponieważ tg α =
	2

3. Pokazujemy, że kąt: ∡APF = 90^o ... można to zrobić na parę sposobów, moja propozycja: I. ∡PAF = 90^o − 2α II. ∡APF = 180^o − (∡PAF + ∡AFP) = 180^o − (90 − 2α + 2α) = 90^o 4. Stąd mamy, że β = α ( ponieważ: β = 90^o − (90^o − α) = α ) 5. Wprowadzamy niewiadomą: |QO| = x

	1
6. korzystając z tego, że tgα = tgβ =		mamy:
	2

|QO| = x −−−> |OR| = 2x −−−> |OF| = 4x ( oczywiście analogicznie także |OP|= 2x ) 7. Tak więc mamy: |AB| = |SF| = |SP| + x + 4x = |SP| + 5x

	1
8. z tgα dla trójkąta ASQ mamy: |SQ| =		|AB| (można też w inny sposób to wyliczyć,
	4

ale tak będzie chyba najszybciej)

	3		3
9. więc mamy: 5x =		|AB| −−−> x =		|AB|
	4		20

10. Liczymy pole:

	1		9
PΔPQR =		|PR|*|QO| = 2x2 =		|AB|2 = 4.5% P□ABCD
	2		200

~~paw:

	9
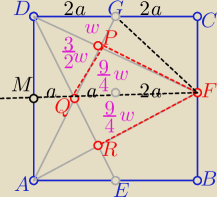
Wykaż, że pole czworokąta FPQR stanowi		pola kwadratu ABCD.
	40

~~paw: tez to zadanie mialem i nie wiem jak

.:

	9
~paw −−− powyżej pokazałem , że pole ΔPQR =		PABCD
	200

	1		1		3
Natomiast PΔPRF =		* |OF| * |PR| =		*4x*4x = 8*(		)2|AB|2 =
	2		2		20

	9
= 4*		|AB|2
	200

	9		9
PPRFQ = PΔPQR + PΔPRF = 5*		PABCD =		PABCD
	200		40

.: Kluczem do zadania jest zauważenie, że:

	1
a) czerwone kąty są równej miary i tgα =
	2

b) niebieskie kąty są równe czerwonym c) stąd masz długości przekątnych tego deltoidu (możesz od razu pole deltoidu liczyć, nie musisz liczyć pól dwóch trójkątów i sumować) d) wyznaczenie z tgα ile wynosi |SQ| pozwala Ci wyliczyć wartość niewiadomej 'x', a w konsekwencji szukane pole deltoidu

Eta:

	3
W trapezie QFGD ΔQFP ∼ΔDPG ( z cechy (kkk) w skali k=
	2

	9
to pole QFP= k2*w =		w, gdzie P(DPG)=w
	4

	3		5
P(DQP)=k*w =		w i P(ADQ)= P(DQG)=
	2		2

	1
To P(ADG)=5w=		P□
	4

	9		9
S= P(FPQR}=2*		=
	4		2

	S		9
zatem:		=
	P□		40

=======

Eta: P_□= 20w

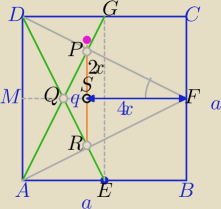Mila: AB=a Nie wiem dlaczego Eta skasowała poprzednie rozwiązanie. Było ładne, ale nie analizowałam końcowego wyniku. Nie było napisane w treści o jakie pole chodzi. α+β=90^o ( popatrz na rysunek) [ABCD]=a², tgα={1}{2} W ΔPQE : (2x)²=q*4x ⇔4x²=q*4x q=x

	5x*4x
[PQRF]=		=10x2
	2

	MQ
2)W ΔMQD: tgα=
	1   a 2

MQ		1		1
	=		, |MQ|=		a⇒
1   ( a)   2		2		4

	3		3
5x=		a ⇔x=		a
	4		20

3)

	9
[PQRF]=10x2=10*		a2
	400

	9
[PQRF]=		a2
	40

========

Simba:

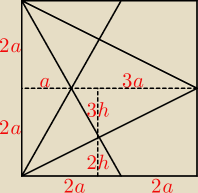
	2		pole deltoidu		2   3* a*3a   5		9
h =		a,		=		=
	5		pole kwadratu		4a*4a		40

Król Lew:

Mila: Super