Ile jest najktótszych dróg z A do B? juli: Ile jest najkrótszych dróg na podanym planie miasta, które prowadzą z punktu A. Licząc to "manualnie", czyli licząc ile jest ścieżek do każdego punktu zaczynając od A wychodzi mi poprawna odpowiedź: 120. Natomiast przy użyciu dwumianu Newtona, już nie koniecznie. Wiem, że najłatwiej jest odjąć liczbę wszystkich dróg od tych przechodzących przez dziure, ale nie wiem jak wyliczyć te przechodzące przez dziurę. Czy ktoś mógłby mnie nakierować?

. : Aby dojść do dziury trzeba wykonać 6 ruchów z czego 2 w górę i 4 w prawo. A z dziury do celu to kolejne 4 ruchy, z czego 2 w górę i 2 w prawo. Ile masz takich dróg?

juli: o mój boźe, nie pomyślałem o tym żeby przechodzić przez punkt postawiony w środku dziury. Teraz pięknie wychodzi i co najważniejsze rozumiem. Dzięki wielkie!

jc: xd

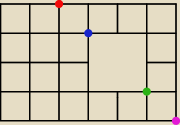
.: Alternatywnym podejściem jest policzenie wszystkich dróg 'wokół' tylko trzeba być dokładnym, aby nie zdublować dróg. Będziesz miał cztery przypadki, każdy z przypadków to dojście do odpowiedniej kropki, a później do celu. Możesz zauważyć, że te kropki (wraz z 'wymazanym punktem) leżą na jednej prostej biegnącej pod kątem 45^o.