próbna nowa era nicklubimie: hej, pisał ktoś dziś rozszerzenie z nowej ery?

próbna: O ten Ci chodzi? https://arkusze.pl/matura-probna-smwp-matematyka-2026-styczen-poziom-rozszerzony/

nicklubimie: nie, z nowej ery

próbna: Masz link? to udostępnij

nicklubimie: wlasnie nie mam, a chcialbym sobie ją przejrzeć

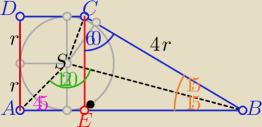
Eta: https://www.youtube.com/watch?v=C_sCYLcMt2w Przeraża mnie to co widzę tu w rozwiązaniu zad.9 Pk=12π⇒ r²=12 Środek okręgu wpisanego znajduje się w punkcie przecięcia dwusiecznych kątów zatem w ΔASB : |∡SAB|=45^o i |∡ASB|=120^o −−− z treści zad to |∡ABS|= 15^o ==a |∡ABC|=2*15^o=30^o w trójkącie "ekierkowym" EBC o kątach ostrych 30^, 60^o ramię |BC|=4r Z warunku wpisania okręgu w trapez a+b= 2r+4r= 6r Pole trapezu :

	a+b
P=		*h= 6r*r=6r2
	2

P=6*12=72 ========= i po ptokach

Eta: Najdłuższa droga jaką "babka" wybrała

Mila: II wariant, jeżeli ktoś nie lubi literek (?) Rysunek i oznaczenia wg Ety.

	a+b
PABCD=		*h
	2

a+b=|CD|+|BC| |AD|=h, |BC|=c h=4√3 W BEC: kąty:30^o, 60^o,90^o ( BS− dwusieczna kąta B ) c=2* 4√3

	4√3+8√3
PABCD=		*4√3=6√3*4√3
	2

P_ABCD=72 ========

chichi: Zadanie dla maturzystów W trójkącie ABC, w którym AB ≠ BC dwusieczną kąta ∡ABC przecina symetralną boku AC w punkcie S. Pokazać, że czworokąt ABCS jest cykliczny.

chichi: Duuuuużo zdrowia dla Was kochane @Eta i @Mila w nowym roku

Mila: Dziękuję pięknie , wzajemnie wszystkiego dobrego życzę. Miło, że pamiętasz.

Eta: Dzięki za pamięć i życzenia Wzajemnie życzę wszystkiego naj,naj.... Pozdrowienia dla Mili

Mila: Cześć, Eto, wszystkiego najlepszego w Nowym Roku

Eta: Hej Tobie też dużo zdrowia w Nowym Roku

Mila: