trapez 123: Punkty A, B, C, D leżą na płaszczyźnie i spełniają warunki: DA = DB = DC, kąt BAC ma miarę 35 stopni, a kąt ABC ma miarę 20 stopni. Udowodnij, że punkty A, B, C, D są wierzchołkami trapezu.

. : Zacznij od tego że D jest środkiem okręgu opisanego na trójkącie ABC Później korzystając z tw o kątach środkowych i opartych na tym samym łuku wykaz że suma odpowiednich kątów jest równa 180^o

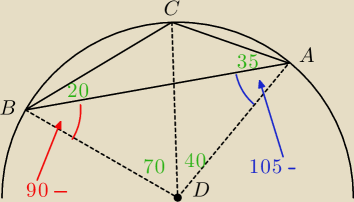
.: Δ_ACD jest równoramienny więc: β = 35 + 105 − β −−−> β = 70 −−−> α = 125 − 70 = 55 I sprawdzasz czy ∡DBC + ∡BCA = 180^o = ∡BDA + ∡DAC

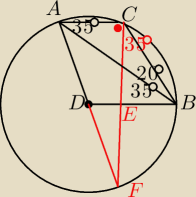
an: Z p/w wynika, że ∡CBE jest prosty, czyli AC||DB, a więc jest to trapez

.: @an ... przeca kąt CBE czyli kąt CBD nie jest kątem prostym

an: tam ma być ∡CEB=90^o

kuta barca: