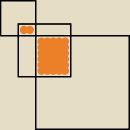
 Dwunastokąt o obwodzie 72 cm jest utworzony z trzech kwadratów, tak jak pokazano na rysunku.
Dwa skrajne kwadraty mają wspólny wierzchołek, a każdy z nich posiada prostokątną część
pokrywającą się (zachodzącą na) ze środkowym kwadratem. Obwód tej części wspólnej jest 5 razy
mniejszy niż suma obwodów jednego kwadratu skrajnego i kwadratu środkowego. Znajdź długość
boku środkowego kwadratu.
Dwunastokąt o obwodzie 72 cm jest utworzony z trzech kwadratów, tak jak pokazano na rysunku.
Dwa skrajne kwadraty mają wspólny wierzchołek, a każdy z nich posiada prostokątną część
pokrywającą się (zachodzącą na) ze środkowym kwadratem. Obwód tej części wspólnej jest 5 razy
mniejszy niż suma obwodów jednego kwadratu skrajnego i kwadratu środkowego. Znajdź długość
boku środkowego kwadratu.
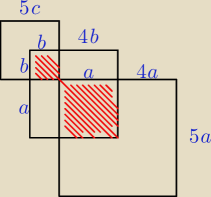 UWAGA
UWAGA  Rysunek nie jest w skali
Rysunek nie jest w skali  Brakuje czegoś w treści zadania ... na chwilę obecną nie można jednoznacznie wyliczyć 'b'
Brakuje czegoś w treści zadania ... na chwilę obecną nie można jednoznacznie wyliczyć 'b'

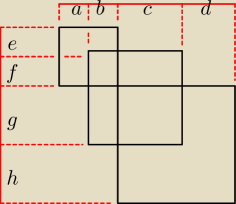 1. Obwcałego = 2*(a+b+c+d+e+f+g+h) = 72 −−−> a+b+c+d+e+f+g+h = 36
2. Środkowy kwadrat ma boki: 'b+c' i 'f+g' więc jego b+c = f+g
3. z warunku o 5 krotnie mniejszym obwodzie:
5*2*(b+f +c+g) = 2*(a+b+c+d +e+f+g+h) −−−−>
4*2*(b+c+f+g) = 2*(a+d +e+h) −−−> 4*(b+c+f+g) = a+d +e+h
4. podstawiamy:
a+b+c+d+e+f+g+h = 4*(b+c+f+g) + b+c+f+g = 36 −−−> 5*(b+c+f+g) = 36 −−−> b+c = 3.6
o 20:43 nie potrafię dzielić przez 20
1. Obwcałego = 2*(a+b+c+d+e+f+g+h) = 72 −−−> a+b+c+d+e+f+g+h = 36
2. Środkowy kwadrat ma boki: 'b+c' i 'f+g' więc jego b+c = f+g
3. z warunku o 5 krotnie mniejszym obwodzie:
5*2*(b+f +c+g) = 2*(a+b+c+d +e+f+g+h) −−−−>
4*2*(b+c+f+g) = 2*(a+d +e+h) −−−> 4*(b+c+f+g) = a+d +e+h
4. podstawiamy:
a+b+c+d+e+f+g+h = 4*(b+c+f+g) + b+c+f+g = 36 −−−> 5*(b+c+f+g) = 36 −−−> b+c = 3.6
o 20:43 nie potrafię dzielić przez 20 
| 1 | 1 | |||
= | *(Obwskrajny 1 + Obwskrajny 2) = | *72 = 14.4 | ||
| 5 | 5 |
| 14.4 | ||
3. Bokśrodkowy = | = 3.6 | |
| 4 |