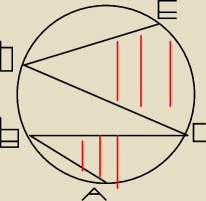
pole okrągu leobuleropl: wierzcholki lamancej abcde nalezą do okregu,katy wpisane BCD mają miare 45 stopni, Udowodnij ze pole figury zakreskowanej czerwoną linia stanowi polowe pola koła.(rys poglądowy)

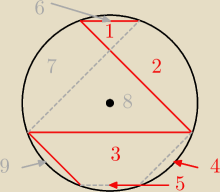.: 1. rotujemy okrąg tak aby BC i DE były poziome (pomaga w zauważeniu rzeczy). 2. rysujemy symetryczne do AB i CD względem pionowej średnicy. 3. pozostawiam Tobie wykazanie dlaczego symetralna (względem poziomej średnicy) będzie AA'. 4. mamy równości pól: P₂ = P₇ ; P₅ = P₆ ; P₄ = P₉ 5. Musimy zatem wykazać jeszcze, że P₃ + P₁ = P₈ A to robimy poprzez zauważenie, że skoro AA' jest symetralną (względem poziomej średnicy) do DE to |AA'| = |DE|. Natomiast ∡CDE = 45^o = ∡ABC (tak samo jak ∡C'D'E' = 45^o = ∡A'B'C') To: P₁ + P₃ = pole trójkąta o podstawie |BC| 6. Teraz wystarczy pokazać, że trójkąt o polu P₈ jest podobny do trójkąta o polu P₁ + P₃ ... a że mają tą samą podstawę (|BC|) to mają takie samo pole

.: alternatywnie pod punktu 5 ... możemy poprowadzić AD i A'E, które są prostopadłe do 'poziomej średnicy' czyli prostopadłe do BC i pokazać które części P₈ będą równe z P₁ i którymi częściami P₃

.: alternatywnie OD* ....

leobuleropl: popraw mnie jesli sie myle,ale twoj rysunek ma zmieniony kąt wpisany C?

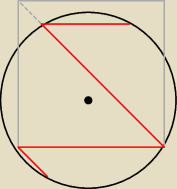
.: z tego co zrozumiałem to masz trzy kąty o mierze 45^o ... przy wierzchołkach B, C i D ... tak Nie przy wierzchołku C masz kąt 45^o ... zobacz rysunek w którym dorysowałem Ci kwadrat. Teraz widzisz, że kąt 45^o jest zachowany

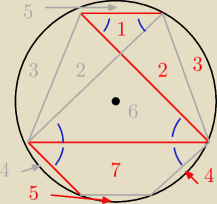.: można też dorobić takie linie (dodatkowo) to ułatwi Ci udowodnienie równości pól które mają te same numery Niebieskie kąty są sobie równe i mają miarę 45^o.

Daniel87: Tylko w twoim rysunku BC i DE są równoległe a rysunek autora jest inny

.: Daniel −−− które kąty mają miarę 45^o Czy są to ∡ABC , ∡BCD , ∡CDE Jeżeli tak to mój rysunek opisuje tą właśnie sytuację. Nie wiem jaki masz rysunek poglądowy i nie jest to istotne ... jeżeli te trzy kąty (które wcześniej wspomniałem) mają miarę 45^o to BC || DE

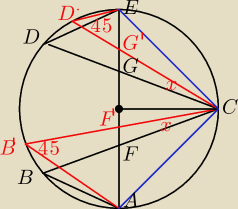an: promień okręgu równy 1, a więc AC=CE=√2 x kąt przesunięcia w okręgu łamanej ABCDE α=22,5^o trójkąty CF'G ;AB'F' ;G'D'E są podobne, ∡ACE=90^o

	1
CG'=
	cos(α+x)

√2		AB'
	=
sin45o		sin(α+x)

AB'=2sin(α+x)

	1
CF'=
	cos(α−x)

√2		D'E
	=
sin45o		sin(α−x)

D'E=2sin(α+x) α=22,5 ⇒sin2(α−x)=sin(45−2x)=cos(45+2x) stosunek sumy pól trójkątów AB'F' oraz G'D'E do CF'G' wyniesie

	AB'		D"E
(		)2+(		)2=sin2(α+x))2+(sin2(α−x))2=(sin (45+2x))2+(cos(45+2x))2=1
	CG'		CF'

czyli zakreskowany obszar jest równy połowie pola okręgu. cnw.