prostokąt Velvet: Spośród wszystkich prostokątów, których pole jest równe P, określ wymiary tego, który ma najmniejszą przekątną.

miękki jak aksamit:

	P
a*b=P ⇒ b=
	a

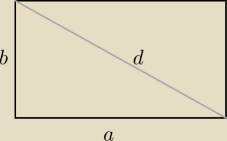
d²=a²+b²

	P2
d2=a2+
	a2

z nierówności między średnimi AM−GM ( lub licz pochodną)

	P2
d2≥ 2√a2*
	a2

d²=2P d=√2P−− wartość najmniejsza to d²a²=a⁴+P² a⁴−2a²P+P²=0 (a²−P)²=0

	P
a=√P i b=		= √P
	√P

takim prostokątem jest kwadrat o boku √P to d= √P*√2= √2P