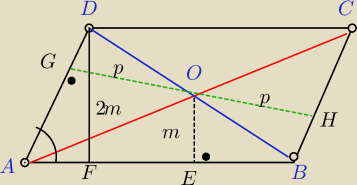
Rownoległobok P i P : W równoległoboku dany jest kąt ostry α i odległości m i p punktu przecięcia przekatnych od nierównych boków . Wyznacz pole i przekątne równoległoboku

	2m		2m
sinα=		to AD=
	AD		sinα

Teraz musze wyliczc długośc boku AB Tylko tutaj jest problem bo GH nie przechodzi przez punkt B aby trójkat AGB był prostokatny bo wtedy bym miał

	2p
sinα=
	AB

P i P : Bo do pola miałbym juz AD i sinα Tylko brakuje AB Przekatne to z twierdzenia cosinusow byl policzyl

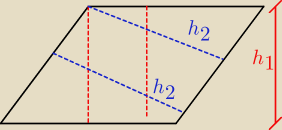.: 1. Wysokość w trapezie (równoległobok jest trapezem) nie musi być opuszczona z wierzchołka aby ją nazywać wysokością 2. A jeżeli tak bardzo chcesz aby wysokość była z wierzchołka B to ją z niej zrób. 3. Zauważ, że przecież nie przedłużałaś EO aby 'mieć wysokość z wierzchołka' ... więc dlaczego oczekiwałeś że przedłużając GO ją otrzymasz

P i P : Rozumiem już widzę . Jakoś dla m wydawało mi sie to naturalne

	2p
AB=
	sinα

S=AD*AB*sinα

	2m		2p		4mp
S=		*		*sinα=
	sinα		sinα		sinα

BD²=AD²+AB²−2AD*AB*cosα

	4m2
BD2=
	4p2   2m   2p   sin2α+ −2* * *cosα   sin2α   sinα   sinα

	4m2+4p2		8mp*cosα
BD2=		−
	sin2		sin2α

	4(m2+p2)−4(2mpcosα)
BD2=
	sin2α

	2√m2+p2−2mpcosα
BD=
	sinα

	2√m2+p2+2mpcosα
Natomiast AC=
	sinα