ciąg Kot:

	n+1
an=
	2n−3

dochodzę do badam monotoniczność

	−5
an+1−an =
	(2n−1)(2n−3)

i liczę (2n−1)(2n−3)>0 co robię źle i dlaczego

.: Ale nie bardzo rozumiem w czym tkwi problem? powinno Ci wyjść, że ten ciąg NIE JEST monotoniczny ponieważ: a₁ = −2 a₂ = 3 (sugeruje ciąg rosnący) a₃ = 4/3 (i dupa ) ciąg ten będzie ciągiem malejącym od n = 2 i taki wniosek powinno się także wyciągnąć sprawdzając dla jakich 'n' zachodzi: (2n−1)(2n−3) > 0

Kot: wychodzi n należy od( −niekończoność do 1/2) suma (3/2 do + niekończoność) i co dalej?

.: więc dla n≥2 mamy mianownik > 0 czyli a_n+1 − a_n < 0 dla n = 1 mamy mianownik < 0 czyli a_n+1 − a_n > 0 wyciągasz wniosek z powyższego

Kot: a dlaczego nie można liczyć tak jak w 19:22

.: Ale możesz ... i 21:02 to wniosek z 19:22 Chyba nie do końca rozumiesz co liczysz i po co to liczysz

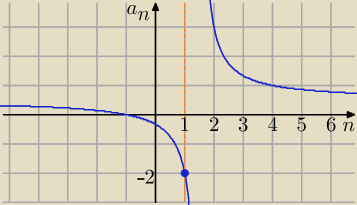
Aaa kotki dwa: dla n=1 ciąg a_n=−2 dla n≥2 ciąg a_n −− jest malejący

Kot: a możesz wyjaśnić skąd z tych przediałów bierze się rozwiązanie?

Jolanta: n to liczby naruralne Mianownik nie może byc równy zero ale może być mniejszy lub większy od zera Zaznacz miejsca zerowe ,narysuj parabole ramionami w gore Jeżeli jest mniejszy od zera n=1 dla n=1 ciąg jest rosnący ujemny licznik przez ujemny mianownik dla n≥2 ciąg jest malejący. Ujemny liczb k przez dodatni mianownik

Kot: dzięki