szybki przykład z wartością bezwzględną
hannah: Hej! Chciałby ktoś proszę na jakimś prostym przykładzie wyjaśnić, jak rozwiązać równanie z
wartością bezwzględną w którym dodajemy dwa wyrażenia pod wartością bezwzględną? tzn np. |x −
4| + |x − 7| = 7 o coś takiego chodzi. Sytuacja w której nie da się wyciągnąć przed znak
wartości bezwzględnej żadnej liczby tak aby te wyrażenia pod wartością bezwzględną były takie
same i aby dało się je po prostu dodać (trochę namieszałam ale mam nadzieję że rozumiecie).
Nigdzie nie mogę znaleźć odpowiedzi..
pozdro

13 paź 19:26
.:
Mamy dwa podejścia ... liczymy (dzieląc na przypadki) ... albo graficznie.
Warto zaznajomić się obydwoma podejściami i wybierać który Ci lepiej pasuje do danego równania.
1. Liczymy
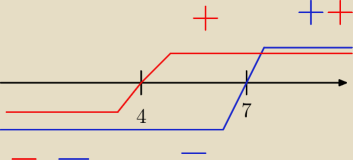
Zaczynamy od narysowania osi X i zaznaczenia punktów w których dochodzi do zmiany znaku w
wartościach bezwzględnych
I widzimy, że będziemy rozdzielać na 3 przypadki:
I. Obie wartości pod wartością są ujemne ... dla x ∊ (−
∞ , 4)
II. Jedna dodatnia, druga ujemna ... dla x ∊ <4 ; 7)
III. Obie dodatnie ... dla x ∊ <7 ; +
∞)
I. x ∊ (−
∞ , 4)
−(x−4) + [−(x−7)] = −x + 4 − x + 7 = −2x + 11
= 7 −−−> 11 − 7 = 2x −−−> x = 2 −−−−
należy do przedziału

II. x ∊ <4 ; 7)
x−4 + [−(x−7)] = x − 4 − x + 7 = 3
= 7 −−−> 0 = 4 −−−> SPRZECZNOŚĆ ... brak rozwiązań w
tym przedziale
III. x ∊ <7 ; +
∞)
x−4 + x−7 = 2x − 11
=7 −−> 2x = 18 −−−> x = 9 −−−− należy do przedziału

ODP: x = 2 ∨ x = 9
13 paź 20:01
moduł:
13 paź 20:02
.:
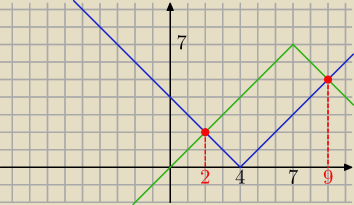
2. Graficznie
wiemy, że wykres f(x) = |x−4| + |x−7| będzie zawierał się w wykresach prostych ... inna prosta
dla innego przedziału (kiedy zmieniamy znak wartości bezwzględnej). Jako, że przez dwa punkty
można poprowadzić tylko jedną prostą to wystarczy policzyć parę wartości tejże funkcji. I np.
robimy:
a) f(4) = 0 + |4−7| = 3
b) f(7) = |7−4| + 0 = 3
c) f(0) = |0−4| + |0−7| = 11
d) f(8) = |8−4| + |8−7| = 4+1 = 5
Zaznaczamy punkty na osi i prowadzimy proste ołówkiem, a długopisem poprawiamy te linie które
należą do danego przedziału.
ZAUWAŻ. Sprawdzając wartość funkcji wziąłem dwa punkty w których zmieniamy znaki w wartości
bezwzględnej, jeden 'na lewo' od obu tych punktów i jeden 'na prawo' od obu tych punktów (te
dwa punkty można sobie wybrać dowolnie oby tylko były odpowiednio na lewo i na prawo od obu
punktów).
Teraz rysujemy prostą
y=7 i odczytujemy z wykresu współrzędną 'x' punktów przecięcia z
wykresem funkcji f(x).
Po odczytaniu współrzędnych 'x' warto je wstawić do równania aby sprawdzić czy się zgadza.
13 paź 20:21
.:
Należy jednak mieć na uwadze, że 'metoda graficzna' nie musi być dokładna (co jeżeli wynikiem
było by x = 2.0001 ∨ x = 8.9999 ... tego byśmy nie zobaczyli rysując.
Ale przy prostych przykładach ... albo dla nas samych ... aby zobaczyć jak to wygląda ... jak
najbardziej jest to coś co bym polecał
13 paź 20:23
.:
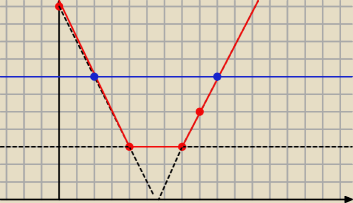
I teraz przy okazji pokazania metody graficznej nauczyciel powinien napomnieć, że na podstawie
wykresu widać, że rozwiązaniem równania:
|x−4| + |x−7| = y (gdzie y to 'jakaś liczba') będziemy mieli :
1. brak rozwiązań (i pokazać, że np. dla y = −1 prosta będzie poniżej wykresu f(x) )
2. dokładnie 2 rozwiązania (i pokazać, że np. y = 7 przecina się dokładnie dwa razy z wykresem
f(x) )
3. nieskończenie wiele rozwiązań (i narysować y=3)
13 paź 20:28
Mila:
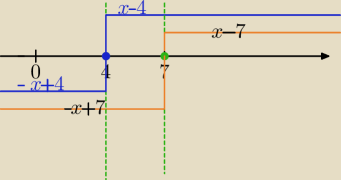
|x − 4| + |x − 7| = 7
1)
|x−4|=x−4 dla x≥4
|x−4|=−x+4 dla x<4
2)
|x−7|=x−7 dla x≥7
|x−7|=−x+7 dla x<7
3) rozwiązujesz równanie w trzech przedziałach ustalając wartości wyrażeń;
1)x<4
(−x+4)+(−x+7)=7 obydwa wyrażenia zmieniły znak
−2x=−4
x=2 ∊D
r
2) x∊<4,7)
x−4+(−x+7)=7
−4=0 dalej sam, powyżej kolega rozwiązał.
Moi uczniowie korzystali z tego sposobu, bo tak opisana oś ułatwiała im pracę.
Niektórzy robili tabelkę:
=====================
13 paź 20:57

 Mamy dwa podejścia ... liczymy (dzieląc na przypadki) ... albo graficznie.
Warto zaznajomić się obydwoma podejściami i wybierać który Ci lepiej pasuje do danego równania.
1. Liczymy
Zaczynamy od narysowania osi X i zaznaczenia punktów w których dochodzi do zmiany znaku w
wartościach bezwzględnych
I widzimy, że będziemy rozdzielać na 3 przypadki:
I. Obie wartości pod wartością są ujemne ... dla x ∊ (−∞ , 4)
II. Jedna dodatnia, druga ujemna ... dla x ∊ <4 ; 7)
III. Obie dodatnie ... dla x ∊ <7 ; +∞)
I. x ∊ (−∞ , 4)
−(x−4) + [−(x−7)] = −x + 4 − x + 7 = −2x + 11 = 7 −−−> 11 − 7 = 2x −−−> x = 2 −−−−
należy do przedziału
Mamy dwa podejścia ... liczymy (dzieląc na przypadki) ... albo graficznie.
Warto zaznajomić się obydwoma podejściami i wybierać który Ci lepiej pasuje do danego równania.
1. Liczymy
Zaczynamy od narysowania osi X i zaznaczenia punktów w których dochodzi do zmiany znaku w
wartościach bezwzględnych
I widzimy, że będziemy rozdzielać na 3 przypadki:
I. Obie wartości pod wartością są ujemne ... dla x ∊ (−∞ , 4)
II. Jedna dodatnia, druga ujemna ... dla x ∊ <4 ; 7)
III. Obie dodatnie ... dla x ∊ <7 ; +∞)
I. x ∊ (−∞ , 4)
−(x−4) + [−(x−7)] = −x + 4 − x + 7 = −2x + 11 = 7 −−−> 11 − 7 = 2x −−−> x = 2 −−−−
należy do przedziału  II. x ∊ <4 ; 7)
x−4 + [−(x−7)] = x − 4 − x + 7 = 3 = 7 −−−> 0 = 4 −−−> SPRZECZNOŚĆ ... brak rozwiązań w
tym przedziale
III. x ∊ <7 ; +∞)
x−4 + x−7 = 2x − 11 =7 −−> 2x = 18 −−−> x = 9 −−−− należy do przedziału
II. x ∊ <4 ; 7)
x−4 + [−(x−7)] = x − 4 − x + 7 = 3 = 7 −−−> 0 = 4 −−−> SPRZECZNOŚĆ ... brak rozwiązań w
tym przedziale
III. x ∊ <7 ; +∞)
x−4 + x−7 = 2x − 11 =7 −−> 2x = 18 −−−> x = 9 −−−− należy do przedziału  ODP: x = 2 ∨ x = 9
ODP: x = 2 ∨ x = 9

 2. Graficznie
wiemy, że wykres f(x) = |x−4| + |x−7| będzie zawierał się w wykresach prostych ... inna prosta
dla innego przedziału (kiedy zmieniamy znak wartości bezwzględnej). Jako, że przez dwa punkty
można poprowadzić tylko jedną prostą to wystarczy policzyć parę wartości tejże funkcji. I np.
robimy:
a) f(4) = 0 + |4−7| = 3
b) f(7) = |7−4| + 0 = 3
c) f(0) = |0−4| + |0−7| = 11
d) f(8) = |8−4| + |8−7| = 4+1 = 5
Zaznaczamy punkty na osi i prowadzimy proste ołówkiem, a długopisem poprawiamy te linie które
należą do danego przedziału.
ZAUWAŻ. Sprawdzając wartość funkcji wziąłem dwa punkty w których zmieniamy znaki w wartości
bezwzględnej, jeden 'na lewo' od obu tych punktów i jeden 'na prawo' od obu tych punktów (te
dwa punkty można sobie wybrać dowolnie oby tylko były odpowiednio na lewo i na prawo od obu
punktów).
Teraz rysujemy prostą y=7 i odczytujemy z wykresu współrzędną 'x' punktów przecięcia z
wykresem funkcji f(x).
Po odczytaniu współrzędnych 'x' warto je wstawić do równania aby sprawdzić czy się zgadza.
2. Graficznie
wiemy, że wykres f(x) = |x−4| + |x−7| będzie zawierał się w wykresach prostych ... inna prosta
dla innego przedziału (kiedy zmieniamy znak wartości bezwzględnej). Jako, że przez dwa punkty
można poprowadzić tylko jedną prostą to wystarczy policzyć parę wartości tejże funkcji. I np.
robimy:
a) f(4) = 0 + |4−7| = 3
b) f(7) = |7−4| + 0 = 3
c) f(0) = |0−4| + |0−7| = 11
d) f(8) = |8−4| + |8−7| = 4+1 = 5
Zaznaczamy punkty na osi i prowadzimy proste ołówkiem, a długopisem poprawiamy te linie które
należą do danego przedziału.
ZAUWAŻ. Sprawdzając wartość funkcji wziąłem dwa punkty w których zmieniamy znaki w wartości
bezwzględnej, jeden 'na lewo' od obu tych punktów i jeden 'na prawo' od obu tych punktów (te
dwa punkty można sobie wybrać dowolnie oby tylko były odpowiednio na lewo i na prawo od obu
punktów).
Teraz rysujemy prostą y=7 i odczytujemy z wykresu współrzędną 'x' punktów przecięcia z
wykresem funkcji f(x).
Po odczytaniu współrzędnych 'x' warto je wstawić do równania aby sprawdzić czy się zgadza.
 |x − 4| + |x − 7| = 7
1)
|x−4|=x−4 dla x≥4
|x−4|=−x+4 dla x<4
2)
|x−7|=x−7 dla x≥7
|x−7|=−x+7 dla x<7
3) rozwiązujesz równanie w trzech przedziałach ustalając wartości wyrażeń;
1)x<4
(−x+4)+(−x+7)=7 obydwa wyrażenia zmieniły znak
−2x=−4
x=2 ∊Dr
2) x∊<4,7)
x−4+(−x+7)=7
−4=0 dalej sam, powyżej kolega rozwiązał.
Moi uczniowie korzystali z tego sposobu, bo tak opisana oś ułatwiała im pracę.
Niektórzy robili tabelkę:
=====================
|x − 4| + |x − 7| = 7
1)
|x−4|=x−4 dla x≥4
|x−4|=−x+4 dla x<4
2)
|x−7|=x−7 dla x≥7
|x−7|=−x+7 dla x<7
3) rozwiązujesz równanie w trzech przedziałach ustalając wartości wyrażeń;
1)x<4
(−x+4)+(−x+7)=7 obydwa wyrażenia zmieniły znak
−2x=−4
x=2 ∊Dr
2) x∊<4,7)
x−4+(−x+7)=7
−4=0 dalej sam, powyżej kolega rozwiązał.
Moi uczniowie korzystali z tego sposobu, bo tak opisana oś ułatwiała im pracę.
Niektórzy robili tabelkę:
=====================