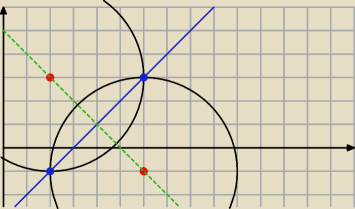
Okrąg 𝑜1 o środku w punkcie 𝑆1 jest określony równaniem (𝑥 − 6)2 + (𝑦 + 1)2 Dominisia: Okrąg 𝑜1 o środku w punkcie 𝑆1 jest określony równaniem (𝑥 − 6)2 + (𝑦 + 1)2 = 16. ⃗⃗⃗⃗⃗⃗⃗⃗ Okrąg 𝑜2 ma środek w punkcie 𝑆2 takim, że 𝑆1𝑆2 = [−4,4]. Promienie tych okręgów są sobie równe. Figura 𝐹 składa się z dwóch okręgów: 𝑜1 oraz 𝑜2. Punkty 𝑀 i 𝑁 są punktami przecięcia figury 𝐹 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 𝐾, leżący na jednej z osi symetrii figury 𝐹, taki, że pole trójkąta 𝑀𝑁𝐾 jest równe 40.

.: 1. zauważ, że wektor S₁S₂ jest pod kątem 135^o = 90^o + 45^o 2. jako, że okręgi jaką takie same promienie oraz z (1) wiemy, że |FK| = |S₁S₂| = r*√2 = 4√2 3. Przyjmuję, że punkt K ma się znajdować na innej osi symetrii niż M i N. 4. Zauważ, że osie symetrii są prostopadłe 5. Niech MN będzie podstawą naszego trójkąta.

	2PΔ		80
6. Związku z tym hΔ =		=		= 10√2
	|MN|		4√2

7. I teraz ... ja bym wyznaczył punkt przecięcia się osi symetrii ... O(4,1) 8. Jako, że oś symetrii która nas teraz interesuje jest pod kątem 135^o to: OK₁ = [10, −10] = K₂O 9. Więc mamy K₁(14,−9) ; K₂(−6,11)

.: oczywiście po punkcie 6 możesz pójść inną drogą wyznaczenia tych współrzędnych punktu K.

.: Zauważ, że ... moje rozwiązanie nie jest OGOLNYM podejściem do problemu ... punkty (1) i (2) mocno ułatwiają całą sprawę i dostosowałem sposób rozwiązania tak aby skorzystać z tego i skrócić żmudne obliczenia do niezbędnego minimum

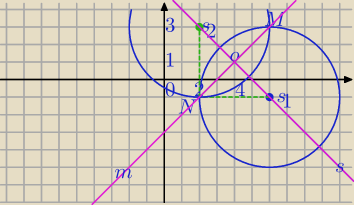
Mila: 1) S₂=(2,3),S₁=(6.−1) równanie okręgu o₂ (x−2)²+(y−3)²=16 Równanie prostej S₁S₂:

	x−2		y−3
S1S2→[−4,4]⇔		=
	−4		4

s: y=−x+5 jedna z osi symetrii 2) punkty przecięcia okręgów: (x−2)²+(y−3)²=16,(x−6)²+(y+1)²=16 N=(2,−1), M=(6,3) O=(4,1)− środek MN Wektor NM^→=[4,4], |MN|=√4²+4²=√32=4√2

	x−2		y+1
Równie osi:		=
	4		4

x−2=y+1 m: y=x−3, a>0 3) P_ΔMNK=40

1
	*4√2*h=40
2

h=10√2 Punkt K ∊prostej s: y=−x+5 K − punkt przecięcia prostej m okręgu o środku O=(4,1) i R=10√2 dokończ sama

Mila: Masz wynik 15: 13 Punkt 9.