kwadraty xxx: Każdy kwadrat na planszy 5x7 jest pomalowany na czerwono lub niebiesko, tak aby każdy kwadrat (czerwony lub niebieski) miał co najmniej dwa sąsiednie kwadraty w kolorze niebieskim. Ile co najmniej niebieskich kwadratów może być na planszy? Wyjaśnienie: Dwa kwadraty są sąsiadujące, jeśli mają wspólny bok.

M:

wredulus_pospolitus: rozumiem, że ten 'każdy kwadrat' jest 1x1, tak

wredulus_pospolitus: Masz wykazać, że dana wartość to najmniejsza możliwa liczba niebieskich kwadratów? Na jakim poziomie nauczania jesteśmy?

xxx: Tak, Tak kwadrat 1x1

wredulus_pospolitus: A dalsze pytania

xxx: Wykazać, że dana wartość to najmniejsza możliwa liczba niebieskich kwadratów Poziom Liceum

wredulus_pospolitus: Dana wartość Czyli znaleźć i wykazać że to jest najmniejsza ... czy masz podaną i masz pokazać, że to jest najmniejsza ? Wygląda mi to na zadanie z OM

: To raczej nie jest zadanie , a szarada. Postawię na 24 niebieskie i 11 czerwonych.

xxx: Może to ktoś rozwiązać?

. : Ale co rozwiązać? Nie odpowiedziałeś na pytania

. : Na dobrą sprawę − pokazać rozstawienie które reprezentuje (naszym zdaniem) sytuację skrajna (najmniejsza liczba niebieskich) jest stosunkowo prosta. Przekazanie toku myślenia dlaczego sądzimy że to jest sytuacja skrajna jest proste. Natomiast formalny dowód to już inna para kaloszy. Najprawdopodobniej musielibyśmy wejść w teorie grafow której oczywiście na poziomie szkoły średniej nie ma

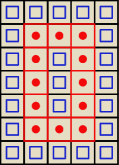
an: 23 niebieskie i 12 czerwonych. Wygląda, że na tej zasadzie można rozwiązać dla dowolnych rozmiarów planszy prostokątnej

. : A − tyle że jest to błędne rozwiązania dwa niebieskie (wewnątrz) sąsiadujące jedynie z jednym niebieskim

. : An*

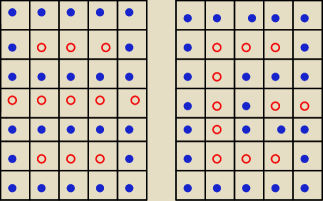
wredulus_pospolitus: to są dwa z wielu różnych rozwiązań dla 11 czerwonych