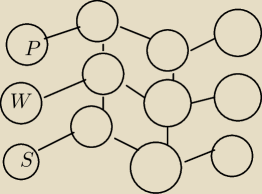
pr-stwo Student: Mając mapę pokoi. Na początku Wojtek znajduje się w pokoju S. Za każdym razem, z takim samym prawdopodobieństwem, przechodzi do innego pokoju, sąsiadującego z obecnym. Jeśli dotrze do pokoju W, od razu wygrywa. Z kolei jeśli dotrze do pokoju P, od razu przegrywa. Poza tym, przemieszcza się, dopóki nie wygra albo nie przegra. Jakie jest prawdopodobieństwo, że Wojtek wygra?

wredulus_pospolitus: a czy Wojtek może wrócić do pokoju w którym już był ?

Student : Nie wiem tego, ja bym założył że nie moze

wredulus_pospolitus: To jest zadanie stworzone przez jakiegoś studenta czy dostałeś na uczelni?

wredulus_pospolitus: Jeżeli nie może wrócić do pokoju w którym był to stwierdzenie: "Poza tym, przemieszcza się, dopóki nie wygra albo nie przegra." nie ma sensu.

wredulus_pospolitus: Ale samo zadanie wtedy można rozwiązać

wredulus_pospolitus: Jeżeli jednak może przejść do innego pokoju to głównym problemem jest to, że przejście do konkretnego pokoju z konkretnego miejsca zależy od tego gdzie się znajdujesz. Natomiast jeżeli zrobisz, że to jest stałe i takie samo, to wtedy prawdopodobieństwo pozostania w pokoju jest różne w zależności od tego gdzie się znajdujemy

wredulus_pospolitus: gdyby i jedno i drugie było jednakowe (co jest niemożliwe ) to wtedy można byłoby to zrobić przy przyjęciu powracania do pokoi

wredulus_pospolitus: dlatego ponawiam pytanie −−− zadanie stworzone przez Ciebie / innego studenta ... czy z zajęć ?

Student: Dopytałem może krążyć między pokojami, nawet w nieskończoność, dopóki nie trafi na W lub P

Student: Mam do tego 5 odpowiedzi a. 7/17 b. 8/17 c. 9/17 d. 10/17 e. 11/17

wredulus_pospolitus: skoro są konkretne odpowiedzi to ile wynosi 'p'

Student : No nie wiem dlatego pytam

wredulus_pospolitus: Student −−− kto to zadanie stworzył ?

Student : No z zajęć a co z nim nie tak