Stereometria
Agnieszka: W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD kąt między sąsiednimi
ścianami bocznymi ostrosłupa ma miarę 120°.
Oblicz stosunek pola powierzchni bocznej tego ostrosłupa do pola podstawy ABCD.
Zapisz obliczenia
22 lip 18:40
wredulus_pospolitus:
Okeeeeeyyy ... i jaki mamy pomysł na to zadanko ?
22 lip 18:46
Agnieszka: próbowałam wszystko uzależnić od jednej zmiennej i potem to podzielić, bo stosunek powinien
raczej wyjść liczbą rzeczywistą, ale mam kłopot, bo nie mogę uzależnić krawędzi ostrosłupa od
krawędzi podstawy, a do tego wysokości ściany bocznej, wysokości pod którą pada kąt i
wysokością ostrosłupa. ktoś dobry z brył pomoże?

bo muszę oddać pracę do standaryzacji
22 lip 18:51
wredulus_pospolitus:
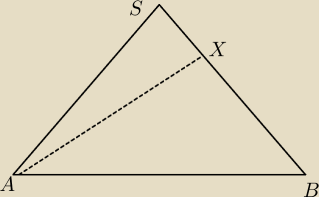
Rysunek przedstawia jedną ścianę boczną.
Na szybkiego (ale będzie trochę roboty z tym):
0. uzależniasz przekątną podstawy od krawędzi podstawy.
1. z tw. cosinusów uzależniasz wysokość ściany bocznej od przekątnej podstawy
2. z tw. pitagorasa (ΔABX) uzależniasz 'część' krawędzi ostrosłupa od podstawy (wykorzystujesz
wysokość ściany bocznej)
3. z tw. pitagorasa (ΔAXC) uzależniasz całość krawędzi wykorzystując pozostałą część krawędzi z
punktu (2).
Ale pewnie jest coś łatwiejszego bo tutaj obliczenia mogą za piękne nie być (chociaż może i nie
... nie liczyłem tego)
22 lip 19:09
Mila:
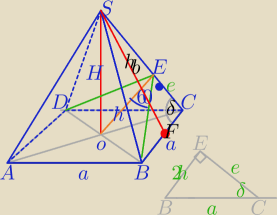
P
b=4*P
BCS
P
ABCD=a
2
BE⊥CS, OE⊥DB
1) W ΔBOE:
|BE|=2h
|OB|=h
√3
|DB|=2h
√3=a
√2
2)
2h
√6=2a
a=h
√6
PABCD=6h2
==========
3) W ΔBCE:
e=h
√2
4)W ΔSFC: h
b
P
ABCD=?
Dokończ, ale posprawdzaj wcześniej rachunki.
22 lip 22:13
Agnieszka: √2
25 lip 15:24
a&b:

25 lip 16:25
 bo muszę oddać pracę do standaryzacji
bo muszę oddać pracę do standaryzacji
 Rysunek przedstawia jedną ścianę boczną.
Na szybkiego (ale będzie trochę roboty z tym):
0. uzależniasz przekątną podstawy od krawędzi podstawy.
1. z tw. cosinusów uzależniasz wysokość ściany bocznej od przekątnej podstawy
2. z tw. pitagorasa (ΔABX) uzależniasz 'część' krawędzi ostrosłupa od podstawy (wykorzystujesz
wysokość ściany bocznej)
3. z tw. pitagorasa (ΔAXC) uzależniasz całość krawędzi wykorzystując pozostałą część krawędzi z
punktu (2).
Ale pewnie jest coś łatwiejszego bo tutaj obliczenia mogą za piękne nie być (chociaż może i nie
... nie liczyłem tego)
Rysunek przedstawia jedną ścianę boczną.
Na szybkiego (ale będzie trochę roboty z tym):
0. uzależniasz przekątną podstawy od krawędzi podstawy.
1. z tw. cosinusów uzależniasz wysokość ściany bocznej od przekątnej podstawy
2. z tw. pitagorasa (ΔABX) uzależniasz 'część' krawędzi ostrosłupa od podstawy (wykorzystujesz
wysokość ściany bocznej)
3. z tw. pitagorasa (ΔAXC) uzależniasz całość krawędzi wykorzystując pozostałą część krawędzi z
punktu (2).
Ale pewnie jest coś łatwiejszego bo tutaj obliczenia mogą za piękne nie być (chociaż może i nie
... nie liczyłem tego)
 Pb=4*PBCS
PABCD=a2
BE⊥CS, OE⊥DB
1) W ΔBOE:
|BE|=2h
|OB|=h√3
|DB|=2h√3=a√2
2)
2h√6=2a
a=h√6
PABCD=6h2
==========
3) W ΔBCE:
e=h√2
Pb=4*PBCS
PABCD=a2
BE⊥CS, OE⊥DB
1) W ΔBOE:
|BE|=2h
|OB|=h√3
|DB|=2h√3=a√2
2)
2h√6=2a
a=h√6
PABCD=6h2
==========
3) W ΔBCE:
e=h√2
