Cięciwy w okręgu
Mila:
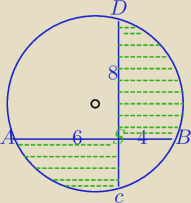
Dla chętnych

Oblicz pole zacieniowanej części koła.
21 lip 16:46
Mariusz:
Na pole całego koła miałbym pomysł
21 lip 17:30
Mila:
Jeśli masz R i pole to dalej można tak:
Podziel cięciwy:
|AB|−4,2,4 i pionową też.
Powodzenia

21 lip 17:37
ABC:
6
2+4
2+8
2+3
2=125 =4R
2
a potem w układ współrzędnych i dla całkownika Mariusza to nie problem

21 lip 19:44
Mila:
Bez całek! To LO.
21 lip 23:04
π: nie ma juz całek w 4 klasie?

22 lip 09:55
Mariusz:
Kiedyś były teraz nie
Jeszcze za czasów gdy chodziłem do szkoły były w szkole średniej choć
tylko w technikach i szkołach policealnych
24 lip 01:59
Velvet: AD=10, BC=4√5, R=2,5√5
Pole=8*4/2+R2/2(α−sinα)+6*3/2+R2/2(β−sinβ)
α=kąt DAB= 2arcsin(DB/2R)
β= kąt ADC= 2π−2arcsin(DC/2R)−2arcsin(AB/2R)
25 lip 22:42
Mariusz:
To trzeba wprowadzić uczniom funkcje odwrotne
Czym jest funkcja różnowartościowa, funkcja "na" , złożenie funkcji , czym jest funkcja na
Ja jeszcze miałem funkcję odwrotną w liceum w podstawie programowej
| | π | | π | |
arcsin(sin(x)) = x , dla x ∊ <− |
| ; |
| > |
| | 2 | | 2 | |
sin(arcsin(x)) = x
26 lip 01:45
Mila:
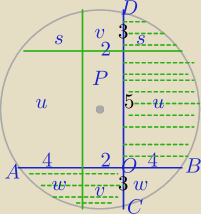
1) 6*4=8*|OC|
|OC|=3
| | 125 | |
R2= |
| − ( ABC 19: 44, (można też inaczej obliczyć ) |
| | 4 | |
P
z=s+u+v+w
2) P=2*5=10
============
26 lip 16:24
SAIzou:
Czy można to wyliczyć korzystając z klasycznego wycinka koła?
Trudno wyznaczyć potrzebne kąty.
26 lip 20:56
Min. Edukacji: @24.07
Gałki były w matfizach w liceum natomiast nie było funkcji odwrotnych, widać to zależało od
nauczyciela.
27 lip 03:22
Mila: Mam inny sposób.wieczorem napisze. Wykorzystać sumę pół odcinków koła.
27 lip 12:08
wredulus_pospolitus:
Miluś ... pragnę tylko zaznaczyć, że na pierwotnym rysunku nie podanego |CO| = 3

27 lip 14:11
Mila:
6*4=8*|OC|
|OC|=3 w pierwszej linijce 16:24
27 lip 14:35
Mila:
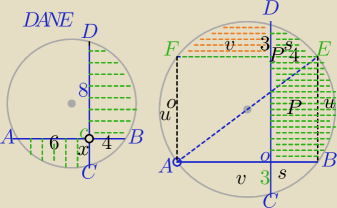
|| sposób
AB⊥CD, |CD|=8, |AC|=6, |CB|=4
Z tw o odcinkach cięciw:
|OC|=3
Szukane : pole zacieniowanego obszaru:
1)
|FE|=|AB| (symetria )
Pola obszarów : AOC i FPD są równe:
|OP|=5, |AB|=10
P
ABCD=10*5=50
W ΔABE z tw. Pitagorasa: 4R
2=125
2) Suma pól odcinków koła:
POle zacieniowanego obszaru jest równe : v+s+u+P
===========
27 lip 15:16
Mariusz:
Min. Edukacji:
Widocznie jesteś już młodszy i wtedy gdy chodziłeś do szkoły materiał był
już pocięty i dlatego nie miałeś funkcji odwrotnych
27 lip 21:10
SAIzou: Ładnie Mila, ja nadal myślę nad kątami, ale nic sensownego nie wychodzi.
28 lip 08:12
Mila:
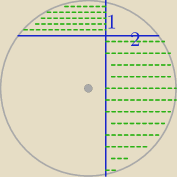
Podobne zadanie ( trudniejsze?)
| | pole zielonej części koła | | 5π−2 | |
Dane : |
| = |
| |
| | pole białej części koła | | 5π+2 | |
Szukane: promień koła.
Powodzenia

28 lip 17:51
dori: Podział podobny jak przy pierwszym, wenetrzny prostokąt dłuższy bok y, krótszy bok x
1⋅(x+1)=2⋅(y+2)
Z=(πR2−xy)/2
B= (πR2−xy)/2+xy
z tw Pit.
x2+(4+y)2=(2R)2
R=2,5√2
29 lip 08:51
dori: Sory dłuższy bok x a krótszy y
29 lip 08:52
SAIzou: Mi wyszło R=√5
29 lip 15:48
29 lip 22:50
SAIzou: Jutro sprawdzę obliczenia, pewnie gdzieś się walnąłem
29 lip 22:55
Mila:

29 lip 23:19
SAIzou: Ale głupi błąd zrobiłem, teraz się zgadza
30 lip 10:17
Mariusz:
ABC gdybym do ciebie napisał prywatną wiadomość na matematyka.pl to czy byś odpisał ?
6 sie 23:07
π: Napisz to się dowiesz

btw. to tu można sobie privy wysyłac?

7 sie 10:33
Mariusz:
Jeżeli chodzi o ten pomysł ABC z całkami to jeżeli przyjmiemy początek układu współrzędnych
w środku okręgu to dostaniemy do policzenia sumę dwóch całek
| | 5 | |
∫−5/211/2(√125/4−y2 − 1)dy + ∫−51(√125/4−x2 − |
| )dx |
| | 2 | |
Jak widać aby znaleźć funkcję podcałkową dla policzenia pola jednego obszaru
wyznaczyłem z równania okręgu x, a aby znaleźć funkcję podcałkową dla policzenia pola
drugiego obszaru wyznaczyłem z równania okręgu y
Całkę z
∫
√R2−x2dx, gdzie R > 0 można policzyć przez części
| | x(−x) | |
∫√R2−x2dx = x√R2−x2 − ∫ |
| dx |
| | √R2−x2 | |
| | −x2 | |
∫√R2−x2dx = x√R2−x2 − ∫ |
| dx |
| | √R2−x2 | |
| | R2−x2−R2 | |
∫√R2−x2dx = x√R2−x2 − ∫ |
| dx |
| | √R2−x2 | |
| | 1 | |
∫√R2−x2dx = x√R2−x2 − ∫√R2−x2dx + R2∫ |
| dx |
| | √R2−x2 | |
| | 1 | |
2∫√R2−x2dx = x√R2−x2 + R2∫ |
| dx |
| | √R2−x2 | |
| | R2 | | 1 | |
2∫√R2−x2dx = x√R2−x2 + |
| ∫ |
| dx |
| | R | | √1−(x/R)2 | |
| | 1/R | |
2∫√R2−x2dx = x√R2−x2 + R2∫ |
| dx |
| | √1−(x/R)2 | |
| | x | |
2∫√R2−x2dx = x√R2−x2 + R2arcsin( |
| )+C1 |
| | R | |
| | 1 | | R2 | | x | |
∫√R2−x2dx = |
| x√R2−x2 + |
| arcsin( |
| )+C |
| | 2 | | 2 | | R | |
27 lis 08:58
bi-elka:
Mariuszek odkopał stary wpis

28 lis 14:16
Mariusz:
O ile się założysz że to ta sama osoba dzieciaku
28 lis 23:34
Mariusz:
A i jak nie masz nic do napisania to po co piszesz
28 lis 23:39
kalkulator: a ty po co

29 lis 13:11
 Dla chętnych
Dla chętnych  Oblicz pole zacieniowanej części koła.
Oblicz pole zacieniowanej części koła.



 1) 6*4=8*|OC|
|OC|=3
1) 6*4=8*|OC|
|OC|=3

 || sposób
AB⊥CD, |CD|=8, |AC|=6, |CB|=4
Z tw o odcinkach cięciw:
|OC|=3
Szukane : pole zacieniowanego obszaru:
1)
|FE|=|AB| (symetria )
Pola obszarów : AOC i FPD są równe:
|OP|=5, |AB|=10
PABCD=10*5=50
W ΔABE z tw. Pitagorasa: 4R2=125
|| sposób
AB⊥CD, |CD|=8, |AC|=6, |CB|=4
Z tw o odcinkach cięciw:
|OC|=3
Szukane : pole zacieniowanego obszaru:
1)
|FE|=|AB| (symetria )
Pola obszarów : AOC i FPD są równe:
|OP|=5, |AB|=10
PABCD=10*5=50
W ΔABE z tw. Pitagorasa: 4R2=125
 Podobne zadanie ( trudniejsze?)
Podobne zadanie ( trudniejsze?)


 btw. to tu można sobie privy wysyłac?
btw. to tu można sobie privy wysyłac? 

