geometria analityczna maturzystka 2025: W kartezjanskim ukladzie wspolrzednych (x,y) dany jest rownoleglobok ABCD o wierzcholkach A= (−8,−1) i D = (−13,9) oraz srodek symetrii M = (−9/2, 1) Okrag O przechodzi przez poczatek ukladu i jest styczny do prostych zawierajacych boki AB i BC tego rownolegloboku .Druga wspolrzedna srodka okregu O jest liczba ujemna . Wyznaczyc rownanie okregu O .

X: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://brainly.pl/zadanie/23214024&ved=2ahUKEwjI7NWSz4KOAxW1HxAIHRFHNusQFnoECB0QAQ&usg=AOvVaw1Hy1_Dlig4HyQUrUBjILQ8

Mila: Z czym masz problem?

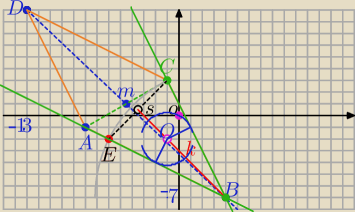
Mila: M = (−9/2, 1), A= (−8,−1) i D = (−13,9) 1) Wsp. punktów B i C M − środek AC

	9		−8+c1		−1+c2
C=(c1,c2) , −		=		i 1=
	2		2		2

⇔ −9=−8+c₁ i 2=−1+c₂ c₁=−1, c₂=3 C=(−1,3) M− środek BD B=(b₁,b₂)

9		−13+b1		9+b2
	=		i 1=
2		2		2

B=(4,−7) 2) Prosta BC: y=−2x+1⇔−2x−y+1=0

	1
Prosta AB:y=−		x−5⇔x+2y+10=0
	2

BC²=125 okrąg ośrodku B i promieniu R=√125

	1
(x−4)2+(y+7)2=125 i prosta y=−		x−5
	2

punkty przecięcia: E=(−6,−2) i F=(14, −12) − pkt F nie odpowiada war. zadania, bo nie leży na boku ΔABC 3) S− środek odcinka EC:.

	7		1
S=(−		,		)
	2		2

Ponieważ ΔBEC jest Δ równoramiennym, to prosta BS jest dwusieczną kąta B 4) Równanie dwusiecznej: BS k: y=−x−3 5) O=(a,b)−Srodek okręgu stycznego do prostych AB i BC leży na dwusiecznej d i jest jednakowo odległy od ramion kąta ABC, od początku układu współrzędnych. O=(a,−a−3) okrąg przechodzi przez punkt (0,0) , druga wsp. ma być ujemna.

	|a+2*(−a−3)+10|
√a2+(−a−3)2=
	√5

	|−a+4|
√2a2+6a+9=
	√5

Poradzisz sobie dalej?

maturzystka 2025: uwazam , ze punkt 3 i 4 sa niepotrzebne . w 5) zmienilam na wspolrzedna b ; bo podane jest b <0)

	| −3+b+10|
√(−3−b)2 +b2 =		, po podniesieniu do kwadratu :
	√5

9b² +16 b −4 + 0⇒ b₁ = −2 , b₂ = 1/9 i a= −1 , r = √a² + b² = √5 (x+1)² + (y+2)² = 5 WIELKIE DZIEKI !

lustfulanchor: Rownoleglobok ABCD w kartezjanskim układzie współrzędnych (x,y) ma wierzchołki A= (−8,−1) i D= (−13,9) oraz środek symetrii M= (−9/2, 1). https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://brainly.pl/zadanie/23214024&ved=2ahUKEwjI7NWSz4KOAxW1HxAIHRFHNusQFnoECB0QAQ&usg=AOvVaw1Hy1_Dlig4HyQUrUBjILQ8 https://elifeonline.io

Lesh George: Great solution, Mila! I agree with maturzystka 2025 about steps 3 & 4 being unnecessary. I got a bit distracted and started thinking about Retro Bowl while working through the coordinate geometry. It seems tedious. https://retrobowl-game.io I got the same final equation of the circle, (x+1)² + (y+2)² = 5.