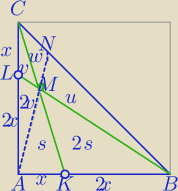
| MB | |
=? | |
| MK |
| CM | LM | |||
2) | =? | =? | ||
| MK | MB |
| 3v+s | x | 1 | |||
= | = | ⇔6v=u+w | |||
| w+u+2s | 2x | 2 |
| LM | v | v | 1 | ||||
= | = | = | |||||
| MB | u+w | 6v | 6 |
| 1 | 7 | |||
LM= | MB⇔ | MB=LB | ||
| 6 | 6 |
| 6 | ||
MB= | √13 | |
| 7 |
| CM | ||
b) | =? | |
| MK |
| 2v | 1 | ||
= | ⇔s=4v | ||
| 3s | 6 |
| CM | w+u | 6v | 3 | ||||
= | = | = | |||||
| MK | 2s | 8v | 4 |
| 3 | ||
CM= | MK | |
| 4 |
| 4 | ||
MK= | x√10 | |
| 7 |
| MB |
| |||||||||||
= | ||||||||||||
| MK |
|
| MB | 3√13 | ||
= | |||
| MK | 2√10 |
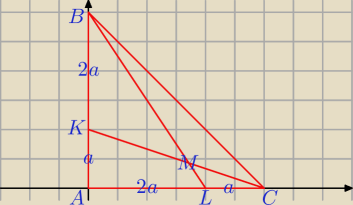 Można i tak: A=(0, 0), L=(2a, 0), C=(3a, 0), K=(0, a), B=(0, 3a)
Można i tak: A=(0, 0), L=(2a, 0), C=(3a, 0), K=(0, a), B=(0, 3a)
| 1 | 3 | |||
prosta KMC: y = − | x+a, prosta BML: y=− | x+3a, | ||
| 3 | 2 |
| 1 | 3 | 12 | 3 | |||||
punkt M: − | x+a=− | x+3a ⇒ M=( | a, | a) | ||||
| 3 | 2 | 7 | 7 |
| |MB| |
| ||||||||||||||||||
( | )2= | = | |||||||||||||||||
| |MK| |
|
| 468 | 36*13 | 9*13 | ||||
= | = | = | ||||
| 160 | 16*10 | 4*10 |