Dziekuje Adam: −Zadanie 1wsze. Dane są przedziały A=(−5,2) B= <0,6> Wyznacz przedziały AU(do góry nogami)B oraz A\B −Zadanie 2gie. Wiosną cenę zimowej kurtki obniżono o 20% i wówczas kosztowała ona 320zł. Oblicz cenę kurtki przed obniżką. −Zadanie 3cie. Wyznacz dziedzinę funkcji f(x) = √x2 − 6x + 9 −Zadanie 4te. Znajdź wzór funkcji, której wykres jest prostą przechodzącą przez punkty ( −1; −4) i ( 0; −3) a. podaj wzór funkcji której wykres jest prostą równoległą do powyższej prostej i przechodzi przez punkt M ( 6; 1) b. Sporządź wykresy obu funkcji na jednym układzie współrzędnych.

Adam: Proszę o pomoc.

Iza: 1.a) Iloczyn A i B to część wspólna obu przedziałów czyli <0;2) b) A\B, czyli A bez B tj. (−5;0) 2. 20% to 1/5 x − cena przed x−1/5x=320 4/5x=320 x=400 3. Działanie pod pierwiastkiem musi być większe bądź równe zeru (oznaczyłam to przez >=. x²−6x+9>=0 Jest to wzór skróconego mnożenia, jest prosty, ale jeśli nie znamy jego pierwiastków liczymy deltę i pierwiastek (albo pierwiastki). Pierwiastkiem tego równ. jest 3. Postać (x−3)²>=0 mówi nam, że pierwiastek jest podwójny, więc się odbija (gdy narysujemy na wykresie widzimy że x należy do R). 4. Piszemy układ równań, podstawiając współrzędne punktów postaci (x,y) do y=ax+b, liczymy a i b. Ostatecznie podstawiamy do wzoru i mamy a)Prosta równoległa musi mieć taki sam współczynnik a, podstawiamy współrzędne punktu M i wyliczamy b i zrobione. b)No tu walnij sobie tabelkę i jedziesz

Adam: dziękuje

Adam: 2. 20% to 1/5 x − cena przed x−1/5x=320 4/5x=320 x=400 nieozumiem jak x− 1/5x ma byc 4/5x ? przeciez sie tego x odejmuje a nie dodaje

Adam: mi w 3ciem wychodzi delta = 72

Iza: Zauważ, że można to rozpisać tak : (1−1/5)x=(5/5 −1/5)x=((5−1)/5)x=4/5x. Delta=b²−4ac, w postaci ax²+bx+c=0, delta w tym przypadku jest równa 0 czyli istnieje tylko jeden pierwiastek, po podstawieniu do wzoru x₀=−b/2a wychodzi 3. Jest to pierwiastek podwójny.

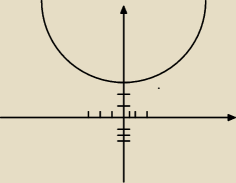
Adam: To ma wyglądac tak? f(x) = √ x² − 6x + 9 x² −6x + 9>0 x₀ = −b/2a x₀ = −6/2 * 1 x₀ − = 3

Iza: Nie musi to dokładny rysunek, nie mogę Ci narysować tego, bo mam problem z myszą, ale chodzi o to że 3 jest pierwiastkiem czyli x−em wiec musisz to zaznaczyć na osi x (tylko ona wystarczy) następnie ustalasz czy a>0 czy a<0 w pierwszym przypadku zaczynasz rysować od góry, w drugim od dołu zawsze od prawej strony, tak by przeszła "falbanka" przez pierwiastek. Jeśli pojawi się potęga przy tym pierwiastku (jak w tym przypadku) to parzysta odbija się(dalej jest nad osią x, taka parabolka), nieparzysta idzie w dół. Teraz sprawdzasz czy funkcja ma być większa od zera czy nie i wybierasz odpowiednią część nad lub pod osią x i zaznaczasz przedziały. W tym przypadku: a>0 funkcja ma być większa bądź równa zeru odbija się przy x=3 co mówi, że jest nad osią x i dokładnie jeden punkt (x=3) jestna osi, więc wszystkie x−sy spełniają równośc. Możemy zapisać, że x należy do R. Troche nagmatwane mam nadzieję, że zrozumiałeś