 Zrobię 'nieszablonowo'.
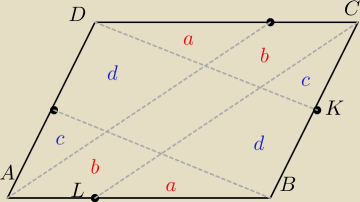
0. Zaznaczamy analogiczne punkty do L i K oraz prowadzimy analogiczne odcinki. W efekcie
uzyskując dwie parę równoległych odcinków.
1. z podobieństwa trójkątów o polu a i a+b mamy:
Zrobię 'nieszablonowo'.
0. Zaznaczamy analogiczne punkty do L i K oraz prowadzimy analogiczne odcinki. W efekcie
uzyskując dwie parę równoległych odcinków.
1. z podobieństwa trójkątów o polu a i a+b mamy:
| 9 | 5 | |||
a+b = | a −−−> b = | a | ||
| 4 | 4 |
| 1 | 9 | |||
3. Z ΔKCD many: PΔKCD = | Prównoległoboku = a+b+c = | a + c | ||
| 4 | 4 |
| 1 | ||
4. Z ΔLBC many: PΔLBC = | Prównoległoboku = a+c+d = a + 4c | |
| 3 |
| 4 | ||
5. Stąd mamy równanie: 9a + 4c = 3a + 12c −−−> a = | c | |
| 3 |
| 9 | 4 | |||
6. Podstawiając do (3) mamy: Prównoległoboku = 4*( | * | + 1)c = 16c | ||
| 4 | 3 |
| a+d |
| 13 | ||||||||||
7. U{PBKML}{Prównoległoboku = | = | = | ||||||||||
| 16c | 16c | 48 |


 Inny sposób.
P− pole równoległoboku ABCD
Inny sposób.
P− pole równoległoboku ABCD
| 1 | ||
(*) PLBC= | P | |
| 3 |
| 3 | ||
1) ΔDMC∼ΔLEM w skali k= | ||
| 5 |
| CM | 3 | ||
= | ⇒ | ||
| ML | 5 |
| PCMB | 3 | 2s | 3 | ||||
= | ⇔ | = | − Δ o tej samej wysokości | ||||
| PLMB | 5 | w | 5 |
| 3 | ||
2s= | w | |
| 5 |
| 3 | 8 | |||
PLBC=2s+w= | w+w= | w | ||
| 5 | 5 |
| 8 | 1 | 5 | |||
w= | P⇔ w= | P | |||
| 5 | 3 | 24 |
| 3 | 13 | 13 | 5 | |||||
PLBKM= | w+w= | w= | * | P | ||||
| 10 | 10 | 10 | 24 |
| 13 | ||
PLBKM= | P | |
| 48 |