Geometria Ks: Bok rombu ABCD ma długość a , a sinus jego kąta ostrego DAB jest równy √(15/4). Na bokach BC i CD wybrano punkty K i L odpowiednio tak, że odcinki AK i AL podzieliły pole rombu ABCD na trzy równe części (zobacz rysunek). https://ibb.co/SXsGHxcL − rysunek Oblicz długość odcinka AL.

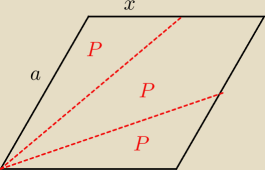
wredulus_pospolitus: 1. P_rombu = a²sin(∡DAB) = a²sin(∡ADC) = 3P

	1		1		1
2, PΔADL =		a*xsin(∡ADC) = P =		Prombu =		a2sin(∡ADC) −−−>
	2		3		3

	2
−−−> 3x = 2a −−−> x =		a
	3

	13		4
3. |AL|2 = a2 + x2 − 2ax*cos(∡ADC) =		a2 −		a2*cos(∡ADC) = (*)
	9		3

4. (∡ADC) > 90^o z jedynki trygonometrycznej:

	15		1		1
1 =		+ cos2(∡ADC) −−−> cos2(∡ADC) =		−−−> cos(∡ADC) = −
	16		16		4

cd (3)

	13		1		16		4
(*) =		a2 +		a2 =		a2 −−−> |AL| =		a
	9		3		9		3

wredulus_pospolitus: taka uwaga −−−> nie √(15/4) (bo to jest >1) tylko √15/4

jubiler: Co to znaczy "odcinki AK i AL podzieliły pole rombu ABCD na trzy równe części"? Brak informacji o równych polach tych części. Czy trzeba się domyśleć, że chodzi o równe pola?

Mila:

	√15
sinα=
	4

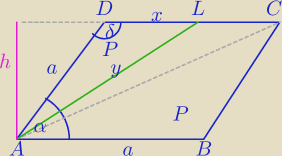
[ABCD]=3P− pole rombu ABCD=3P 1)

	1		3		3		1
[ACD|=		*3P=		P, [ALC]=		P−P=		P
	2		2		2		2

Trójkąty mają taką samą wysokość. 2)

[ADL]		P		2		2
	=		=		⇔x=		a
[ALC]		1   P 2		1		3

	1		1
3) cosα=		( jak wyżej) , cosδ=−
	4		4

	4		2		1
y2=a2+		a2+2*a*		a*
	9		3		4

	4
y=		a
	3

=======

Mila: ad jubiler, masz napisane, że odcinki podzieliły pole...