dowod geometryczny
matematycznyswir: W trójkącie równoramiennym ABC z wierzchołka A poprowadzono wysokość która przecięła odcinek BC
w punkcie D, w taki sposób, że |BD|: |DC| = 1: 2. Następnie z wierzchołka B również
poprowadzono wysokość, która przecięła odcinek AC w punkcie E, takim, że |AE|: |EC| = 1: 2.
Wysokości przecięły się w punkcie F. Udowodnij, że |BC||FD|=3√52
11 maj 18:35
Zosia:
x
2+b
2=y
2 i (x+y)
2+(2b)
2=(3b)
2
(y−x)(y+x)=b
2 i x+y=
√5b
i y+x=
√5b
dokończ...
otrzymasz tezę
11 maj 19:45
Zosia:
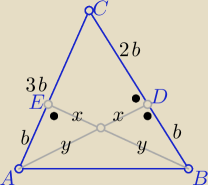
Pominęłam punkt F na rys.
x=|FD|
11 maj 19:47
matematycznyswir: Dziękuję ślicznie!
11 maj 20:17
 x2+b2=y2 i (x+y)2+(2b)2=(3b)2
(y−x)(y+x)=b2 i x+y=√5b
x2+b2=y2 i (x+y)2+(2b)2=(3b)2
(y−x)(y+x)=b2 i x+y=√5b