styczna do wykresu funkcji matematycznyswir: Dana jest funkcja określona wzorem: f(x) = √5−x² , gdzie x∈[−√5, √5]. Wyznacz równania stycznych do wykresu funkcji f, które są prostopadłe do prostej o równaniu y=2x+5. Wyliczyłem pochodną, przyrównałem ją do −0.5, wyszły mi dwa x0: −1 i 1. Z tego wyszły mi również dwa równania stycznych: y=−0.5x+1.5 oraz y=−0.5x+2.5 −− wg odpowiedzi tylko pierwsze z nich jest poprawną odpowiedzią. Dlaczego?

M:

ABC: wyszły mi dwa x0: −1 i 1 tu jest źle , zapewne wprowadziłeś obcy pierwiastek podnosząc do kwadratu matematyczny świr takie rzeczy powinien mieć w małym paluszku

wredulus_pospolitus: świr −−−> 1. Funkcja f(x) jest parzysta 2. Zauważ, że funkcja f(x) jest malejąca dla x<0 ; a rosnąca dla x>0 3. Jak bardzo byśmy się 'pobawili' to możemy policzyć f''(x) i pokazać, że f''(x) < 0 dla dowolnego x∊D_f'' Na podstawie punktów (2) i (3) wiemy, że rodzina stycznych do wykresu f(x) = √5−x² NIE BĘDZIE posiadała dwóch równoległych. Związku z tym tylko co najwyżej jedna styczna może być prostopadła do zadanej prostej. Zastanów się dlaczego tylko połączenie punktów (2) i (3) daje nam tą pewność. Jak również − co tak naprawdę w (2) jest istotne dla nas (bo na pewno nie to w jakim konkretnie przedziale jest ona malejąca).

matematycznyswir: Nie wiem czy dobrze myślę, ale może punkty 2. i 3. sugerują, że wykres funkcji to fragment wykresu funkcji kwadratowej, która nigdy nie będzie miała dwóch stycznych równoległych? Proszę poprawcie mnie, jeśli wypisuję herezje. Dodam, że sprawdziłem teraz f'(x) dla swoich dwóch punktów x0 i wyszło mi, że f'(1)=−0.5 ale f'(−1)=0.5, co jest niezgodne z wartością współczynnika kierunkowego stycznej, która ma być prostopadła do prostej y=2x+5. To zdecydowanie odrzuca mi x0=−1. Nie wiem jak mogłem to przeoczyć. Tak jak napisał ABC − faktycznie nieuważnie podniosłem do kwadratu, stąd moje zapytanie: jak rozwiązać to inaczej bez takich komplikacji? Teoretycznie mając równanie 2x=√5−x² mógłbym narysować wykresy tych funkcji w układzie współrzędnych i tak odczytać x0, ale nie wiem czy nie znalazłby się inny, szybszy sposób.

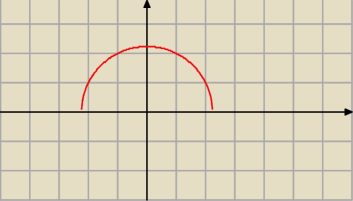
wredulus_pospolitus: tak wygląda wykres funkcji f(x) jak widzisz ... współczynnik kierunkowy stycznej będzie ujemny dla x>0 f(x) = √5−x² f'(x) = U{−x}{√5−x²

wredulus_pospolitus: co więcej −−− z wykresy wynika, że styczna nie może posiadać b = 1.5

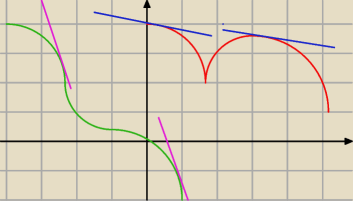
wredulus_pospolitus: a co do punktów 2 i 3 ... popatrz na te dwie funkcje: g(x) nie spełnia (2) warunku przez co istnieją dwie styczne o tym samym współczynniku kierunkowym h(x) nie spełnia (3) warunku przez co także istnieją dwie styczne o tym samym współczynniku kierunkowym Natomiast gdy gdy możemy zapisać za pomocą jednego przedziału (a,b) przedział w którym funkcja maleje, a w (c,d) rośnie i jednocześnie (de facto) nie ma punktów przegięcia (czyli w danym przedziale monotoniczności funkcja jest tylko wklęsła lub tylko wypukła) to taka sytuacja nie będzie miała miejsca. I to właśnie dotyczy naszej funkcji f(x).

matematycznyswir: Faktycznie. Wykres funkcji jednak dużo mi rozjaśnił, będę pamiętać aby sobie w taki sposób sprawdzać te styczne. Dziękuję!

wredulus_pospolitus: a co do samego wykresu f(x). y = √5−x² −−−> y² = 5−x² (dla y≥0) −−−> x² + y² = 5 (dla y≥0) co by było alternatywną drogą rozwiązania tego zadania bez użycia pochodnej i wzoru na styczną. Bo wtedy: h(x) || 2x+5 i przechodzi przez środek półokręgu −−−> h(x) = 2x Punkt przecięcia z półokręgiem (czyli punk styczność szukanej stycznej): (1,2) −−−> styczna: g(x) = −0.5x + 2.5